Chapitre 7 Tests statistiques pour des variables qualitatives

7.1 Test du \(\chi^2\) d’adéquation (ou encore dit de conformité ou d’ajustement)

7.1.1 Calculs sous-jacents

Le test du \(\chi^2\) d’adéquation consiste à comparer la distribution d’une variable qualitative observée avec une distribution théorique. Pour mieux voir en quoi cela consiste, prenons un exemple repris de Danielle Navarro (2018) où l’on chercherait à savoir si, lorsqu’on demande à des personnes de choisir “au hasard” mentalement une carte parmi un ensemble de cartes étalées devant soi, le choix se fait vraiment de manière entièrement aléatoire. Pour étudier cela, on demande à 200 personnes de réaliser l’expérimentation et on note le type de carte qui a été retenu : coeur, trèfle, carreau, ou pique. Le jeu de données est crée avec le code ci-dessous :

# Creation du jeu de données
trefles <- rep("trèfles", 35)
carreau <- rep("carreau", 51)
coeur <- rep("coeur", 64)
pique <- rep("pique", 50)

cartes <- data.frame(
  id = seq(1, 200, 1), 
  choix = c(trefles, carreau, coeur, pique)
  )

Dans ce cadre, l’idée que les personnes choisiraient leur carte purement au hasard (idée ou hypothèse qu’on va noter \(H_{0}\)) se traduit par le fait que chaque type de carte aurait la même probabilité d’être tiré à chaque fois, soit une chance sur quatre (0.25). Le vecteur \(P\) qui résumerait les probabilités, pour les différents types de carte, d’être choisi à chaque choix d’une personne serait alors le suivant :

\[H_{0} : P = (0.25, 0.25, 0.25, 0.25).\]

Étant donné qu’il y a 200 personnes (\(N\)) dans notre exemple, la distribution théorique \(E\) des fréquences de tirage de chaque type de carte qui correspondrait à l’hypothèse \(H_{0}\) serait telle que \(E = N \cdot P\), soit :

\[E = (50, 50, 50, 50).\]

On peut aussi mettre cela sous forme de vecteur avec R :

expected <- c("carreau" = 50, "coeur" = 50, "pique" = 50, "trefles" = 50)
expected

## carreau   coeur   pique trefles 
##      50      50      50      50

Maintenant que l’on connaît la distribution théorique correspondant à notre exemple, voyons qu’elle est la distribution réelle obtenue suite à notre expérimentation. Pour l’obtenir, on peut résumer la variable choix du jeu de données cartes crée juste précédemment, cela grâce à la fonction table() :

# Vue numérique de la distribution observée
observed <- table(cartes$choix)
observed

## 
## carreau   coeur   pique trèfles 
##      51      64      50      35

# Vue graphique de la distribution observée
cartes %>% 
  group_by(choix) %>% 
  count(choix) %>% 
  ggplot(aes(x = choix, y = n)) + 
  geom_bar(stat = "identity")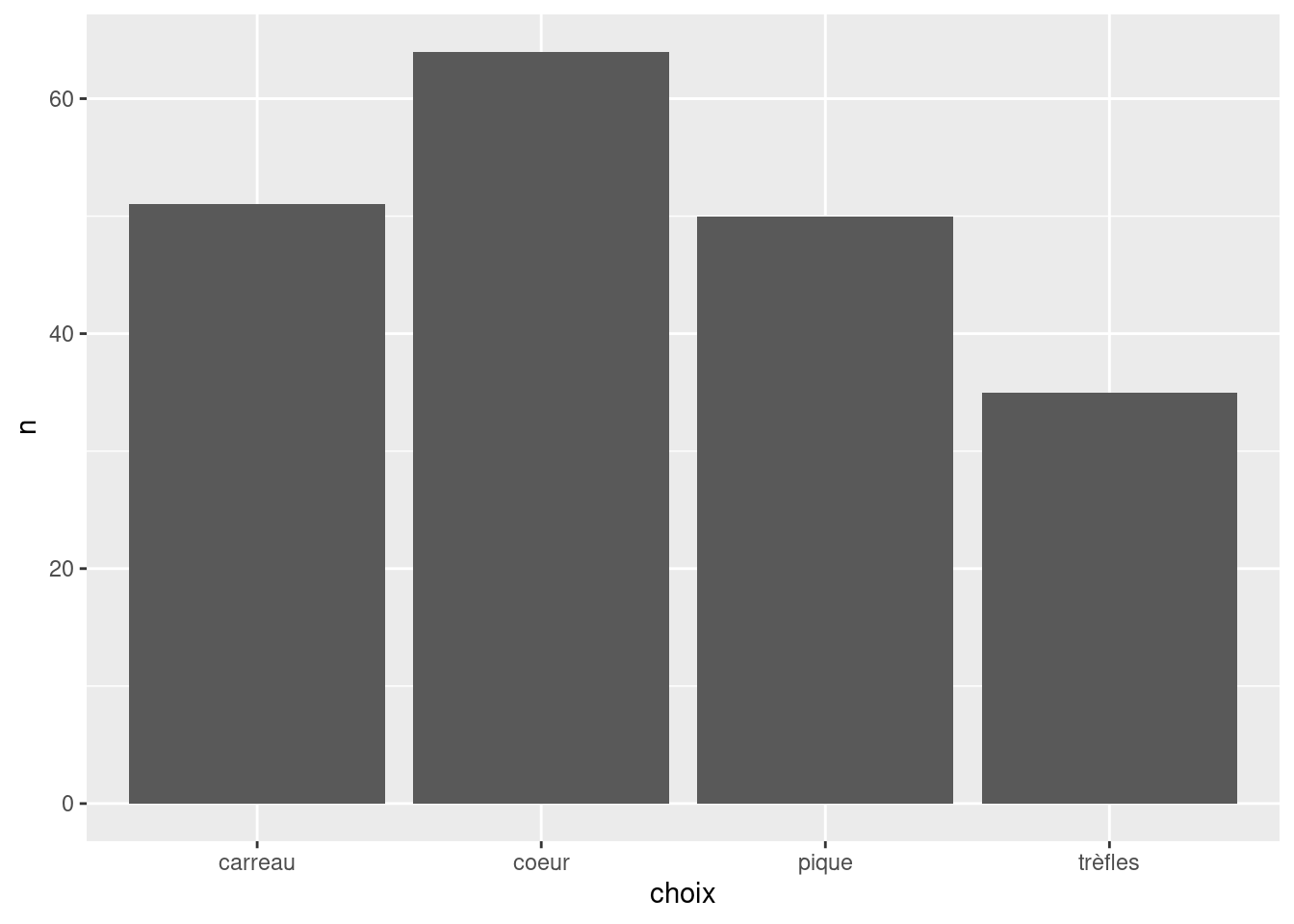

Figure 7.1: Visualisation des fréquences dans le jeu de données cartes

La distribution \(O\) des fréquences observées pourrait s’écrire comme suit : \[O = (51, 64, 50, 35)\]

À présent, il convient de calculer une statistique qui résumerait l’écart qu’il peut y avoir entre la distribution théorique, et celle observée. Cette statistique, c’est \(X^2\) ou \(GOF\) (pour Goodness Of Fit), tel que :

\[X^2 = \sum_{i=1}^{k} \frac{(O_{i} - E_{i})^2}{E_{i}},\]

\(k\) étant le nombre total de modalités de la variable (ici les types de cartes), \(O_{i}\) désignant la fréquence pour la \(i\)-ème modalité de la variable observée, et \(E_{i}\) désignant la fréquence pour la \(i\)-ème modalité de la variable théorique. On peut calculer \(X^2\) manuellement :

sum((observed - expected)^2 / expected)

## [1] 8.44

Nous avons à présent le score qui résume l’écart obtenu entre la distribution observée et la distribution théorique de notre variable qualitative. Il nous reste alors à connaître la distribution d’échantillonnage de la statistique \(X^2\) dans le cas où \(H_{0}\) serait vraie. Cela nous permettra de connaître la probabilité de rencontrer une valeur de \(X^2\) au moins aussi grande que 8.44 dans le cas où \(H_{0}\) serait vraie, et de juger ainsi si cette probabilité supporte ou non \(H_{0}\)… Trêve de suspens, la distribution d’échantillonnage de \(X^2\) suit une loi \(\chi^2\) à \(k-1\) degrés de liberté (\(k\) étant le nombre de types d’évènement possibles, ici les types de cartes tirées). Comment peut-on expliquer cela? Tout d’abord, reprenons le calcul de \(X^2\), et plus précisément le terme \(O_{i}\). Admettons qu’il ne concerne qu’un seul type de cartes (e.g., les cœurs). Ce terme a sa propre distribution de probabilité en posant que \(H_{0}\) soit vraie, et cette distribution est celle d’une loi binomiale (avec \(\theta\) = 0.25 et \(N\) = 200 dans notre exemple), puisque pour chaque sujet interrogé, il était possible que ce type de carte soit choisi, ou non. Or, il s’avère que lorsque \(N\) est relativement grand et que \(\theta\) n’est ni trop proche de 0, ni trop proche de 1, la distribution se rapproche d’une loi normale (Navarro, 2018). En allant vite, pour un type de cartes donné, on peut alors considérer que l’expression \(\frac{(O_{i} - E_{i})}{E_{i}}\) a une distribution d’échantillonnage qui s’apparente à une loi normale standard, et c’est le cas à chaque fois que cette expression doit être reprise pour chaque type de carte. Si on met au carré chacune de ces variables, puis qu’on les additionne (comme décrit plus haut pour le calcul de \(X^2\)), on se retrouve dans la situation dans laquelle nous obtenons une loi \(\chi^2\) (cf. chapitre Prérequis). La subtilité ici, par rapport au chapitre Prérequis, est que le nombre de degrés de liberté n’est pas \(k\) mais \(k-1\). Le nombre de degrés de liberté désigne le nombre de quantités distinctes à décrire (ici 4 quantités car les données sont regroupées en 4 modalités) moins le nombre de contraintes (ici 1 contrainte liée au groupe de sujets qui a un nombre fini). On a donc bien 3 degrés de liberté ici car il nous suffit de connaître le score de fréquence de 3 modalités pour connaître le score de fréquence de la 4ème modalité qu’il nous manquerait pour une taille d’échantillon donnée.

La Figure 7.2 montre la loi \(\chi^2\) relative à 3 degrés de liberté et donc les probabilités de rencontrer tel ou tel intervalle de valeurs de \(X^2\) dans le cas où notre \(H_{0}\) serait vraie. La zone hachurée représente la probabilité qui était d’obtenir une valeur de \(X^2\) au moins aussi grande que 8.44 dans l’hypothèse où \(H_{0}\) serait vraie. Cette probabilité \(P\) est de 3.8 %. En principe, lors d’un test statistique, il y a aussi ce qu’on appelle une “région critique”, c’est-à-dire l’intervalle dans lequel la valeur de la statistique de test, ici \(X^2\), devrait se trouver pour qu’on considère que nos résultats ne supportent pas \(H_{0}\) et donc qu’on ne retienne pas cette hypothèse. Classiquement (voire par défaut, à tort), cette région critique est définie à l’aide du seuil \(P <= 0.05\). Dans le cas présent, cela se traduirait par le fait que notre statistique \(X^2\) tomberait dans l’intervalle pour lequel il y avait une probabilité inférieure ou égale à 5 % de tomber dans le cas où \(H_{0}\) serait vraie. Dans notre exemple, cela se traduirait par le fait d’obtenir une valeur de \(X^2\) supérieure ou égale à environ 7.81. La région critique correspondant à cette zone est montrée en rouge sur la Figure 7.2. En suivant cette démarche, dans le cas présent \(H_{0}\) serait donc bien rejetée puisque notre valeur \(X^2\) de 8.44 tomberait dans la région critique. Le test serait alors dit “significatif”.

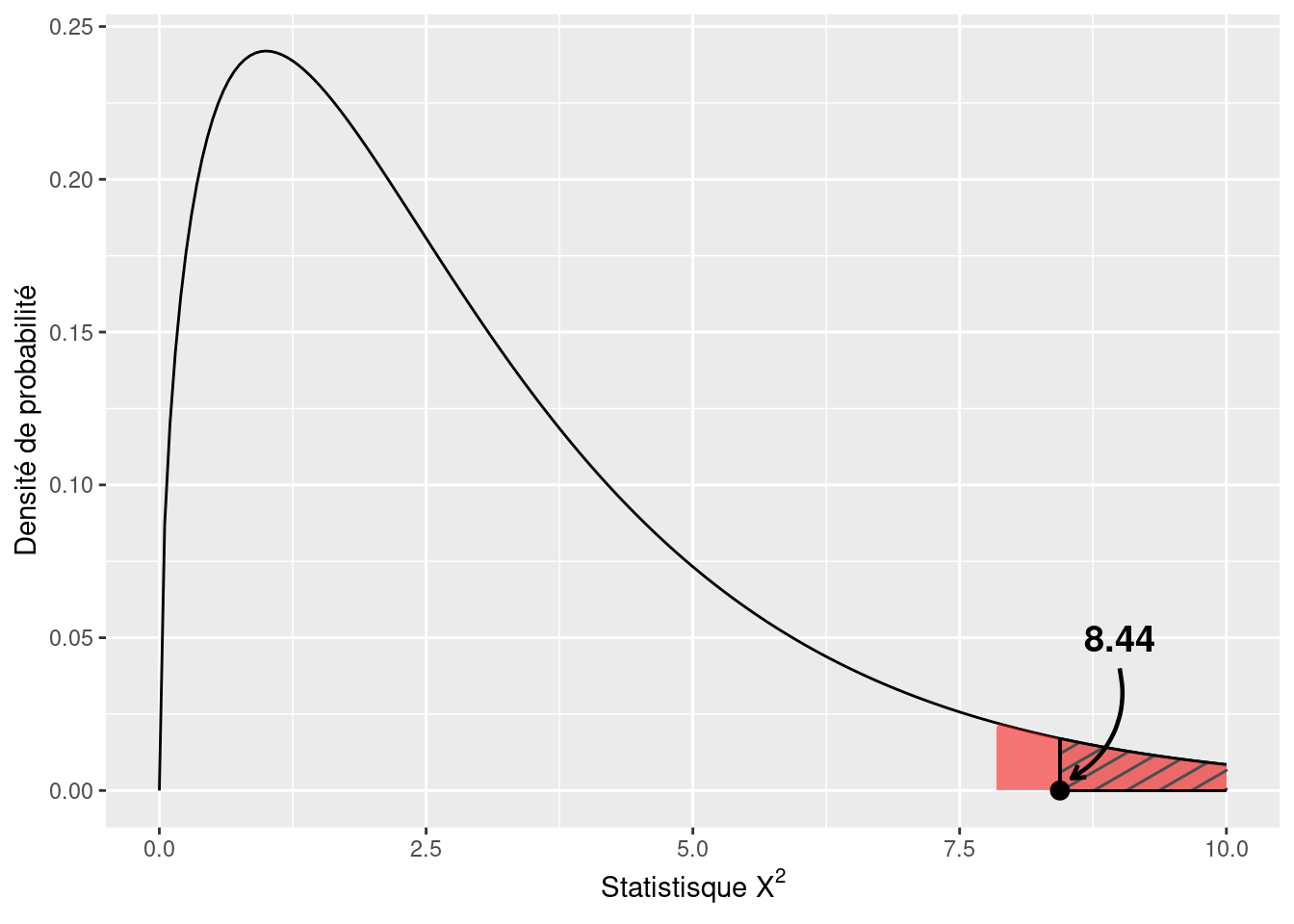
Figure 7.2: Distribution d’échantillonnage de la statistique \(X^2\) sous \(H{0}\)

7.1.2 Application avec R

Nous venons de voir la mécanique des calculs qu’il y a derrière le test \(\chi^2\) d’adéquation. Heureusement, il existe des fonctions dans R pour faire cela automatiquement, comme la fonction chisq.test() :

observed <- table(cartes$choix)
expected <- c(0.25, 0.25, 0.25, 0.25)
chisq.test(x = observed, p = expected)

## 
##  Chi-squared test for given probabilities
## 
## data:  observed
## X-squared = 8.44, df = 3, p-value = 0.03774

Une seconde fonction possible est la fonction goodnessOfFitTest() du package lsr. Elle est intéressante en raison du fait qu’elle propose un récapitulatif plus détaillé de la configuration du test qui a été faite. De plus, pas besoin de passer par la fonction table(), mais il faut que la variable étudiée soit en format factor :

lsr::goodnessOfFitTest(as.factor(cartes$choix), p = c(0.25, 0.25, 0.25, 0.25))

## 
##      Chi-square test against specified probabilities
## 
## Data variable:   as.factor(cartes$choix) 
## 
## Hypotheses: 
##    null:        true probabilities are as specified
##    alternative: true probabilities differ from those specified
## 
## Descriptives: 
##         observed freq. expected freq. specified prob.
## carreau             51             50            0.25
## coeur               64             50            0.25
## pique               50             50            0.25
## trèfles             35             50            0.25
## 
## Test results: 
##    X-squared statistic:  8.44 
##    degrees of freedom:  3 
##    p-value:  0.038

Pour reporter les résultats, nous pourrions écrire les choses comme cela (Navarro, 2018) : Le résultat du test était significatif (\(\chi^2(3)\) = 8.44, \(P\) = 0.04). Ainsi, on considère que nos données ne supportent pas suffisamment l’hypothèse initiale selon laquelle il y aurait une probabilité identique pour chaque type de carte d’être tiré par une personne. Le choix d’une carte par une personne ne serait donc pas réellement aléatoire.

Il convient de noter que les probabilités espérées (théoriques) peuvent être définies à volonté selon la question de recherche. Par exemple, on aurait pu tester l’hypothèse \(H_{0}\) selon laquelle les personnes préfèrent à 80 % les cœurs, 10 % les trèfles, 5 % les piques, et 5 % les carreaux. Le tout est de bien configurer le test pour que les fréquences observées pour chaque modalité (ici les types de cartes) soient bien mises en correspondance avec les fréquences théoriques (ces dernières étant configurées à l’aide de l’argument p dans l’exemple de code ci-dessous). La fonction lsr::goodnessOfFitTest() a donc un fort intérêt ici pour bien vérifier, dans les résultats affichés, qu’on a bien attribué les probabilités théoriques aux bonnes modalités) :

lsr::goodnessOfFitTest(as.factor(cartes$choix), p = c(0.05, 0.8, 0.05, 0.1))

## 
##      Chi-square test against specified probabilities
## 
## Data variable:   as.factor(cartes$choix) 
## 
## Hypotheses: 
##    null:        true probabilities are as specified
##    alternative: true probabilities differ from those specified
## 
## Descriptives: 
##         observed freq. expected freq. specified prob.
## carreau             51             10            0.05
## coeur               64            160            0.80
## pique               50             10            0.05
## trèfles             35             20            0.10
## 
## Test results: 
##    X-squared statistic:  396.95 
##    degrees of freedom:  3 
##    p-value:  <.001

7.2 Test du \(\chi^2\) d’indépendance (ou d’association)

library(catdata)
data("encephalitis")
encephalitis

##    year country count
## 1     1       1     1
## 2     1       2     2
## 3     2       1     0
## 4     2       2     1
## 5     3       1     1
## 6     3       2     2
## 7     4       1     2
## 8     4       2     5
## 9     5       1     2
## 10    5       2     4
## 11    6       1     3
## 12    7       1     8
## 13    8       1     5
## 14    8       2     6
## 15    9       1    13
## 16    9       2     7
## 17   10       1    12
## 18   10       2     7
## 19   11       1     6
## 20   11       2     7
## 21   12       1    13
## 22   12       2     3
## 23   13       1    10
## 24   13       2     4
## 25   14       1    12
## 26   14       2     2

(en cours…)

7.3 Résumé

• Le test du \(\chi^2\) d’adéquation consiste à comparer une distribution observée à une distribution théorique qui représenterait l’hypothèse à tester.
• La statistique de test du \(\chi^2\) d’adéquation est \(X^2\) et suit une distribution \(\chi^2\).
• La fonction R de base pour réaliser le test du \(\chi^2\) d’adéquation est chisq.test().
• Une fonction R très aidante pour réaliser correctement le test du \(\chi^2\) d’adéquation est lsr::goodnessOfFitTest().