Skip to main content

Analyser des données avec R

Chapitre 4 Analyses bivariées

Réaliser une analyse bivariée désigne le fait d’étudier la relation qui peut exister entre deux variables. Dans ce chapitre, nous allons voir les procédures graphiques et calculatoires qui permettent d’étudier et de quantifier le degré de relation pouvant exister entre deux variables dans les cas suivants : entre deux variables quantitatives, entre deux variables qualitatives, et entre une variable quantitative et une variable qualitative. Comme dans le chapitre précédent, l’objectif est ici d’explorer et de décrire les données et leurs relations à l’échelle d’un échantillon, sans pour autant chercher à déterminer l’incertitude qu’il peut exister dans les statistiques calculées en vue de les utiliser pour réaliser une inférence dans la population représentée.

4.1 Relation entre deux variables quantitatives

4.1.1 Étudier graphiquement la relation

Comme dans le cadre d’analyses univariées, une bonne pratique, lorsqu’on étudie une relation bivariée, est de faire un graphique. Avec des variables quantitatives, il s’agit de montrer les valeurs d’une variable en fonction des valeurs de l’autre variable, chose que permet un simple nuage de points. Plusieurs types de relations peuvent alors être rencontrés, ces relations pouvant potentiellement s’apparenter à autant de fonctions mathématiques que l’on connaît. Parmi les plus connues, on a par exemple les relations linéaires, les relations logarithmiques, ou encore les relations quadratiques, qui sont illustrées sur la Figure 4.1.

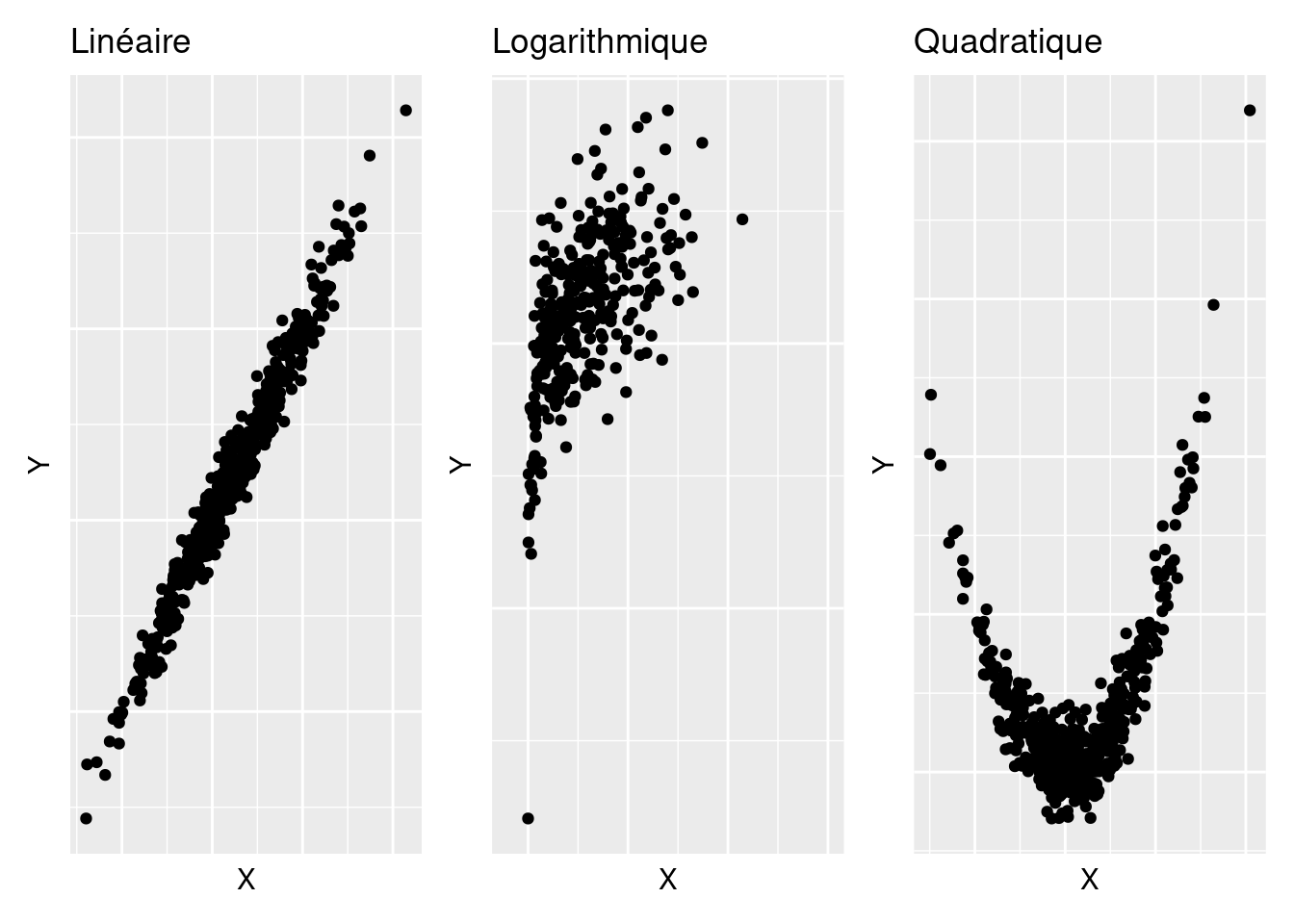
Différentes formes de relation entre deux variables quantitatives

Figure 4.1: Différentes formes de relation entre deux variables quantitatives

Avec R, pour obtenir un nuage de points à partir d’un jeu de données, il est possible d’utiliser la fonction ggplot() en l’associant à la fonction geom_point() du package ggplot2, comme dans l’exemple ci-dessous qui utilise le jeu de données mtcars (qui est intégré à R de base) et les variables hp (gross horsepower) et mpg (miles/US gallon). Dans cet exemple dont le résultat est montré sur la Figure 4.2, on peut voir que la relation semble globalement linéaire négative (voire curvilinéaire négative si l’on donne de l’importance au point isolé à droite du graphique).

ggplot(data = mtcars, aes(x = hp, y = mpg)) + 
  geom_point()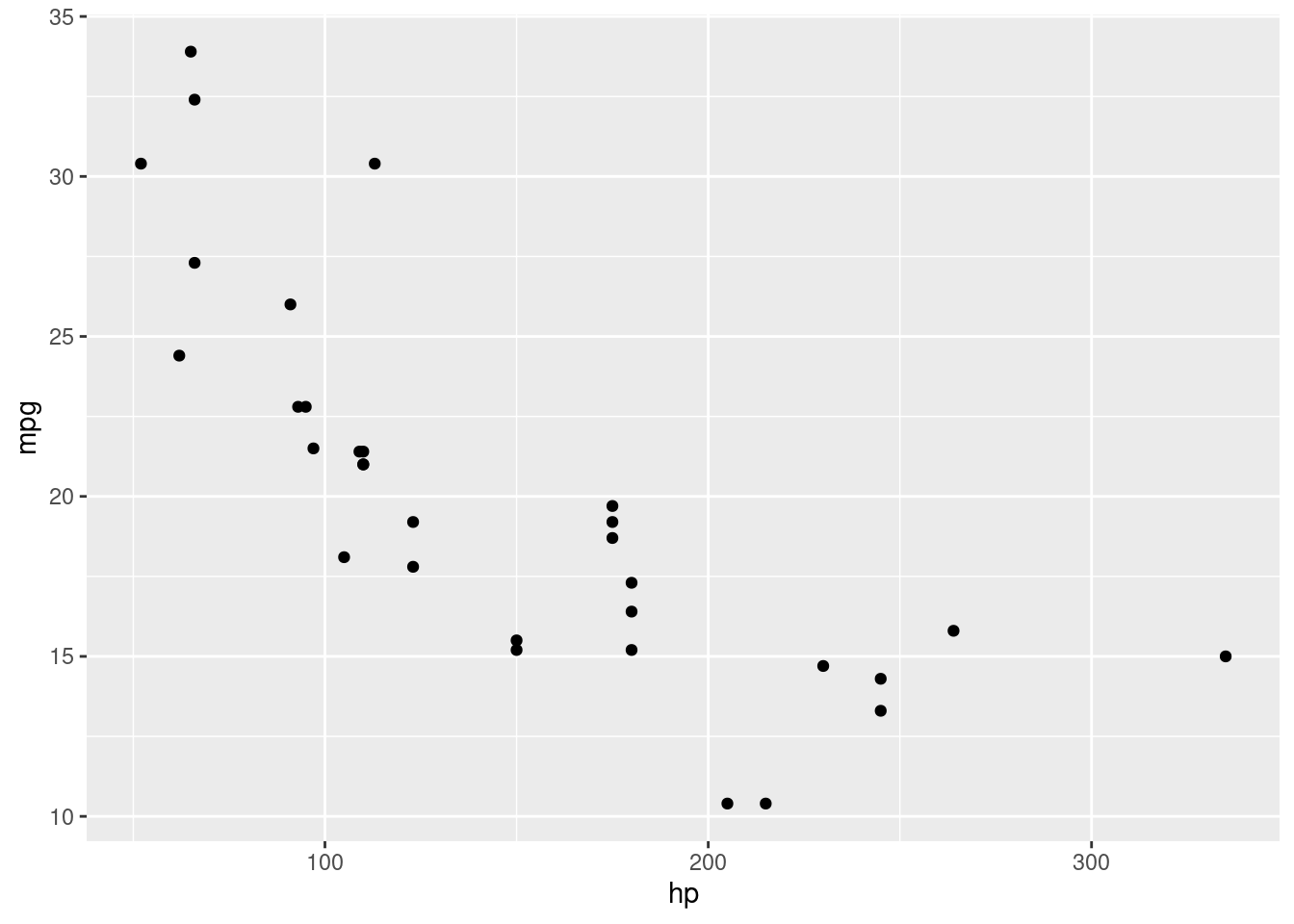
Nuage de points montrant les variables hp et mpg du jeu de données mtcars

Figure 4.2: Nuage de points montrant les variables hp et mpg du jeu de données mtcars

4.1.2 Étudier numériquement la relation

Le coefficient de corrélation de Pearson

Lorsque la relation étudiée semble linéaire, l’étude numérique classique consiste à calculer le coefficient de corrélation de Pearson, noté \(r\), dont la valeur vise à renseigner dans quelle mesure le nuage de points représentant le lien entre les deux variables étudiées suit une droite. Avant de se lancer dans le calcul du coefficient de corrélation de Pearson pour étudier la relation entre une variable \(X\) et une variable \(Y\), il peut donc être utile de compléter le nuage de points montré sur la Figure 4.2 avec une droite d’équation de type \(Y = aX + b\). Cette équation serait la meilleure modélisation possible de la relation linéaire entre \(X\) et \(Y\), de telle sorte que parmi l’infinité d’équations qui pourraient lier \(X\) à \(Y\), c’est cette équation qui au total donnerait la plus petite erreur lorsque l’on voudrait prédire \(Y\) à partir de \(X\). Si \(X\) et \(Y\) sont liées de manière linéaire, alors le nuage des points relatifs aux deux variables devrait s’étaler le long de cette droite. Pour obtenir cette droite en plus du nuage de points, il est possible d’utiliser la fonction geom_smooth() du package ggplot2.

ggplot(data = mtcars, aes(x = hp, y = mpg)) + 
  geom_point() +
  geom_smooth(formula = y ~ x, method = "lm", se = FALSE)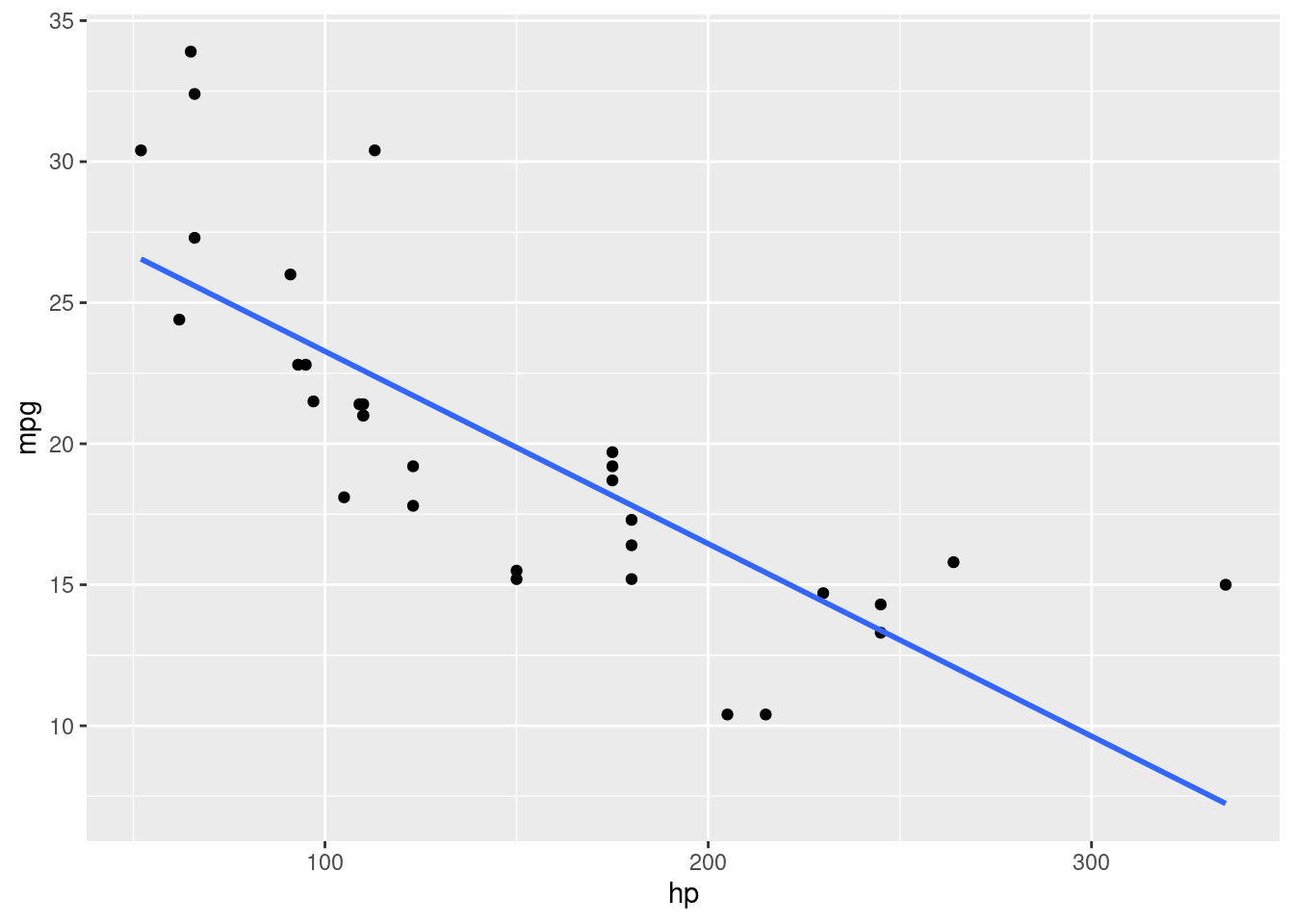
Nuage de points avec droite de régression pour les variables hp et mpg du jeu de données mtcars

Figure 4.3: Nuage de points avec droite de régression pour les variables hp et mpg du jeu de données mtcars

Dans la fonction geom_smooth() qui a été utilisée dans l’exemple ci-dessus, on note que l’argument formula pourrait être considéré comme facultatif car il s’agit ici de la configuration par défaut de la fonction. En revanche, l’argument method doit être ici configuré avec "lm" (pour linear model) car ce n’est pas la méthode graphique configurée par défaut dans la fonction. Enfin, l’argument se permet de montrer ou non un intervalle de confiance autour de la droite de régression, ce qui n’a pas été activé ici (par défaut, l’argument se est configuré pour montrer cet intervalle de confiance). Dans l’exemple montré ci-dessus, la représentation graphique encourage fortement à penser que l’un des types de relations à envisager prioritairement dans l’étude des deux variables est la relation linéaire. Cette information rend pertinente l’utilisation du coefficient de corrélation de Pearson pour une étude numérique de la relation en question.

La valeur du coefficient de corrélation de Pearson peut aller de 1 (suggérant une relation linéaire positive parfaite) à -1 (suggérant une relation linéaire négative parfaite). Des valeurs proches de 0 suggèreraient une abscence de relation linéaire. La formule du coefficient de corrélation de Pearson (\(r\)) pour un échantillon est la suivante :

\[r_{X,Y} = {\frac{COV_{X,Y}}{\hat{\sigma}_{X} \hat{\sigma}_{Y}}} = {\frac{\sum_{i=1}^{N} (X{i} - \overline{X}) (Y{i} - \overline{Y})}{N-1}} {\frac{1}{\hat{\sigma}_{X} \hat{\sigma}_{Y}}},\]

\(COV\) désignant la covariance entre les variables \(X\) et \(Y\), \(X{i}\) et \(Y{i}\) les valeurs de \(X\) et \(Y\) pour une observation \(i\), \(\overline{X}\) et \(\overline{Y}\) les moyennes respectives des variables \(X\) et \(Y\), \(N\) le nombre d’observations, et \(\hat{\sigma}_{X}\) et \(\hat{\sigma}_{Y}\) les écarts-types respectifs des variables \(X\) et \(Y\). Cette formule indique que le coefficient de corrélation de Pearson s’obtient en divisant la covariance des deux variables étudiées par le produit de leurs écarts-types respectifs.

Le Tableau ?? montre les premières étapes du calcul de la covariance pour des couples de variables fictifs \((X1,Y1)\), \((X1,Y2)\), et \((X1,Y3)\). En particulier, la partie droite du tableau (de X1Y1 à X1Y3) montre le calcul du produit \((X{i} - \overline{X}) (Y{i} - \overline{Y})\) pour les différents couples de variables et cela pour chaque ligne du jeu de données.

``` ```{=html}
(\#tab:tablecov)Étape intermédiaire pour le calcul de la covariance entre des variables X1 et Y1, Y2, et Y3

X1

Y1

Y2

Y3

X1Y1

X1Y2

X1Y3

0

0

0

0

36

40.285714

-36

2

2

1

-2

16

22.857143

-16

4

4

15

-4

4

-16.571429

-4

6

6

5

-6

0

0.000000

0

8

8

11

-8

4

8.571429

-4

10

10

3

-10

16

-14.857143

-16

12

12

12

-12

36

31.714286

-36

Ce que ce tableau montre, c’est que plus les deux variables étudiées évolueront de manière consistante dans des sens identiques comme avec \(X1\) et \(Y1\), ou de manière consistante dans des sens opposés comme avec \(X1\) et \(Y3\), plus les produits \((X{i} - \overline{X}) (Y{i} - \overline{Y})\) donneront respectivement des grands scores positifs ou des grands scores négatifs, et moins les scores \((X{i} - \overline{X}) (Y{i} - \overline{Y})\) à additionner pour le calcul de la covariance s’annuleront. En effet, avec une relation relativement linéaire et positive les scores seront plus systématiquement positifs, et avec une relation relativement linéaire et négative les scores seront plus systématiquement négatifs. Toutefois, lorsqu’on aura des variables qui n’évolueront pas de manière consistante dans le même sens ou dans un sens opposé comme avec \(X1\) et \(Y2\), les scores positifs et négatifs liés aux calculs \((X{i} - \overline{X}) (Y{i} - \overline{Y})\) auront tendance à s’annuler et donneront lieu à une somme des scores \((X{i} - \overline{X}) (Y{i} - \overline{Y})\) diminuée, et donc à une covariance et à un coefficient de corrélation de Pearson tirés vers 0. Ces différents cas de figure et les calculs \((X{i} - \overline{X}) (Y{i} - \overline{Y})\) correspondants sont illustrés sur la Figure 4.4. Sur cette figure, chaque carré correspond au calcul \((X{i} - \overline{X}) (Y{i} - \overline{Y})\), le carré étant bleu lorsque le résultat du calcul est positif, et rouge lorsque le résultat est négatif. L’aire d’un carré illustre la grandeur du score issu du calcul. Sur les graphiques de gauche et de droite de la figure, on distingue une relation linéaire parfaite, ce qui maximise les scores à additionner pour le calcul de la covariance, dans le positif pour le graphique de gauche et dans le négatif pour le graphique de droite. Sur le graphique du milieu, on remarque que le manque de relation linéaire donne lieu à des carrés à la fois bleus et rouges, indiquant que les scores associés aux calculs \((X{i} - \overline{X}) (Y{i} - \overline{Y})\) de la covariance s’annulent et diminuent ainsi la valeur finale de la covariance.

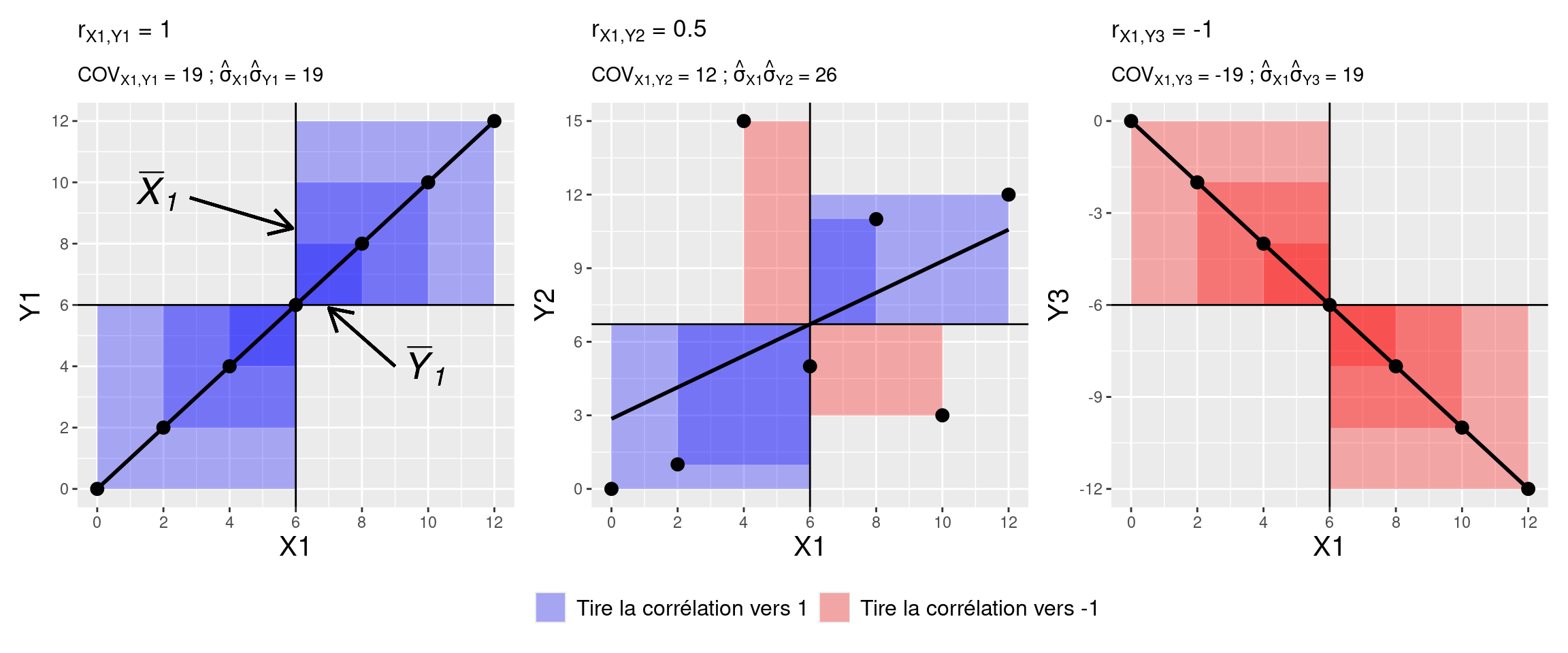
Illustration du calcul de la covariance

Figure 4.4: Illustration du calcul de la covariance

Dans R, le coefficient de corrélation de Pearson peut être obtenu avec la fonction cor(). Dans l’exemple ci-dessous qui reprend les variables du jeu de données mtcars utilisées plus haut, on observe un coefficient négatif, relativement proche de -1, suggérant une relation relativement linéaire et négative entre les variables étudiées.

cor(x = mtcars$hp, y = mtcars$mpg, method = "pearson")
## [1] -0.7761684

Toutefois, la fonction cor.test() sera plus intéressante pour la suite car elle permet de calculer des indices statistiques de probabilité qui seront nécessaires dès lors qu’il s’agira de chercher à inférer la valeur d’une corrélation dans une population d’où l’échantillon étudié provient. La valeur de la corrélation est donnée à la fin de la liste des informations qui apparaissent suite à l’activation de la fonction.

cor.test(x = mtcars$hp, y = mtcars$mpg, method = "pearson")
## 
##  Pearson's product-moment correlation
## 
## data:  mtcars$hp and mtcars$mpg
## t = -6.7424, df = 30, p-value = 1.788e-07
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.8852686 -0.5860994
## sample estimates:
##        cor 
## -0.7761684

Sur la base de travaux antérieurs, Hopkins et al. (2009) ont fait une proposition de classification pour qualifier la valeur du coefficient de corrélation qui serait obtenue dans le cadre d’une relation linéaire. Cette proposition est montrée dans le Tableau ?? :

``` ```{=html}
(\#tab:correlationtable)Termes caractérisant la taille de l'effet en fonction de la valeur de corrélation obtenue

Petite

Moyenne

Grande

Très grande

Extrêmement grande

0.1

0.3

0.5

0.7

0.9

Pour visualiser le lien que l’on peut faire entre la forme du nuage de points et la valeur du coefficient de corrélation de Pearson que l’on peut obtenir, la page web proposée par Kristoffer Magnusson (https://rpsychologist.com/correlation) peut être particulièrement intéressante. Cette page web donne la possibilité de faire varier manuellement la valeur du coefficient de corrélation de Pearson pour ensuite voir un nuage de points type correspondant à cette valeur. Faites un essai !

À noter que la valeur du coefficient de corrélation de Pearson est dépendante du degré de dispersion des valeurs autour de la tendance centrale (Halperin, 1986). Ceci est illustré sur la Figure 4.5. À gauche de la figure, on observe un nuage de points représentant une relation obtenue entre deux variables quantitatives dans une population complète. La valeur du coefficient de corrélation de Pearson est ici particulièrement élevée. À droite de la figure, on observe exactement les mêmes variables dans la même population que sur le graphique de gauche, mais sur un intervalle dont l’étendue a été manuellement restreinte, diminuant ainsi la variabilité pour les deux variables. On observe alors une diminution de la valeur du coefficient de corrélation de Pearson. Cet exemple doit faire prendre conscience qu’il faut faire attention lorsqu’on cherche à comparer des coefficients de corrélation de Pearson obtenus avec des échantillons différents. En effet, si les variables correspondant respectivement à ces échantillons n’ont pas les mêmes niveaux de variabilité, les valeurs des coefficients de corrélation de Pearson ne seront pas vraiment comparables, en sachant que c’est l’échantillon qui présente la plus grande variabilité qui aura plus de chances de présenter une valeur de coefficient de corrélation de Pearson plus élevée.

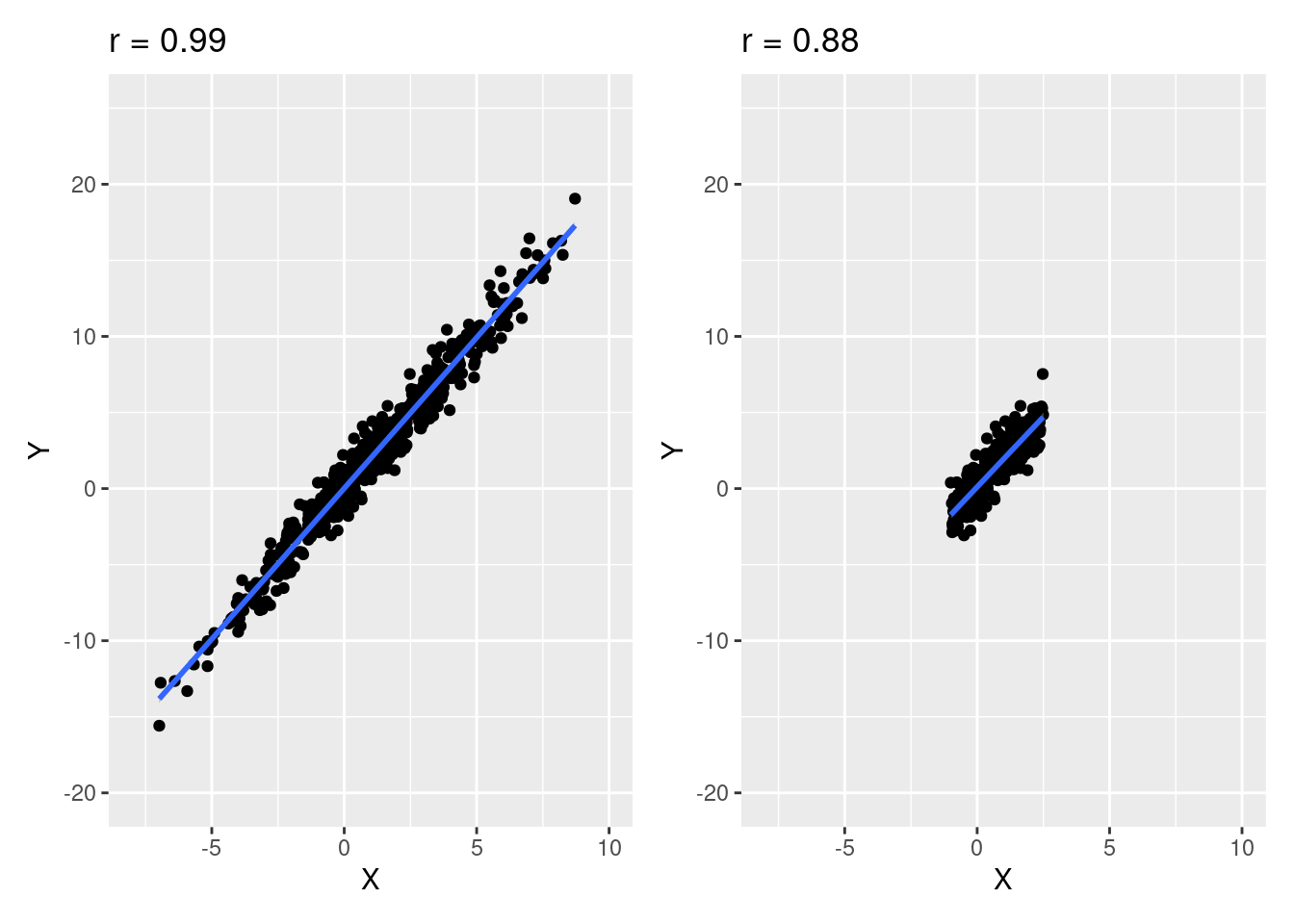
Influence de la diminution de l'étendue des variables sur la valeur du coefficient de corrélation de Pearson

Figure 4.5: Influence de la diminution de l’étendue des variables sur la valeur du coefficient de corrélation de Pearson

Un cas particulier illustrant l’influence du degré de dispersion sur la relation étudiée est montré sur la Figure 4.6. Cet exemple a pour but de montrer que l’étude d’une relation entre deux variables quantitatives peut aboutir à des conclusions radicalement différentes selon que l’on conduit les analyses à l’échelle d’un groupe entier ou que l’on sépare les analyses par groupe de caractéristiques, en particulier lorsque la distribution des données par groupe est radicalement différente de celle obtenue à l’échelle du groupe entier. Sur la gauche de la Figure 4.6, le nuage de points représente la relation entre deux variables à l’échelle de l’ensemble du groupe étudié. La variabilité possible pour les deux variables étudiées (V1 et V2 dans l’exemple) est alors maximale. Toutefois, ces données appartiennent en réalité à des sous-groupes distincts (cf. couleurs sur le graphique de droite de la Figure 4.6). L’analyse par sous-groupe diminue la variabilité à la fois pour V1 et V2, donnant même lieu ici à des relations de sens opposé à celui observé à l’échelle de l’ensemble du groupe ! Cette situation correspond à ce qu’on appelle un paradoxe de Simpson, lequel se présente lorsque le phénomène que l’on peut observer avec une vue globale est annulé voire inversé lors d’une analyse par sous-groupe. Ici, la grande variabilité associée aux données du graphique de gauche de la Figure 4.6 crée une relation artificiellement et donc faussement positive entre V1 et V2. C’est l’analyse par sous-groupe qui permet de révéler la vraie nature de la relation étudiée.

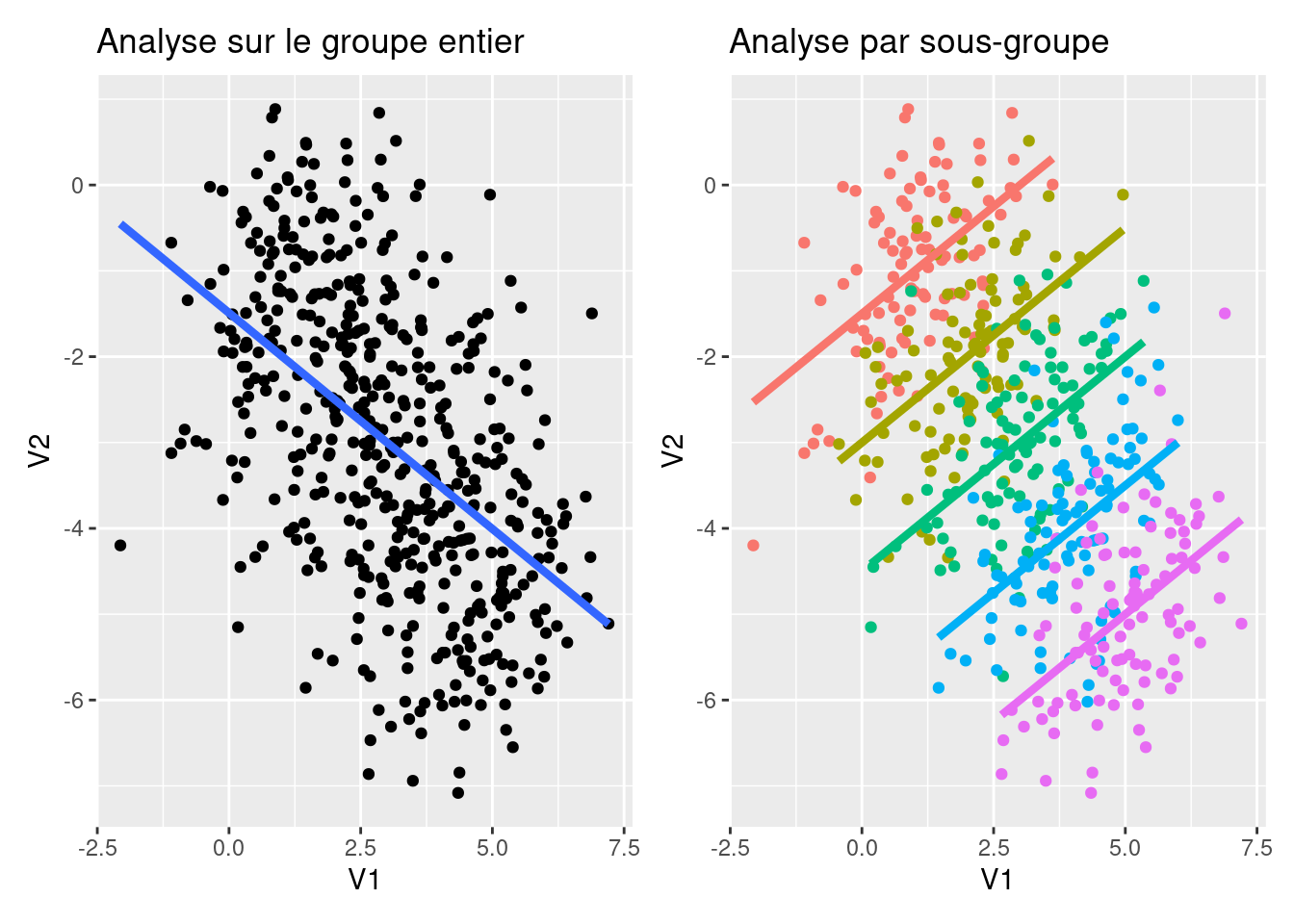
Influence du niveau d'analyse (groupe entier vs. sous-groupes) sur la corrélation observée entre deux variables quantitatives

Figure 4.6: Influence du niveau d’analyse (groupe entier vs. sous-groupes) sur la corrélation observée entre deux variables quantitatives

En outre, la valeur du coefficient de corrélation de Pearson peut être influencée par des valeurs extrêmes, comme montré sur la Figure 4.7. Les deux graphiques de cette figure montrent exactement les mêmes données, à ceci près que sur le graphique de droite, on a remplacé en ordonnées une valeur du graphique de gauche pour lui donner la valeur de 10. L’influence de cette simple action sur la valeur du coefficient de corrélation de Pearson est nette. Ceci montre qu’il faut faire attention aux valeurs extrêmes qui pourraient grandement influencer la variabilité des données d’une variable et au final la valeur de corrélation obtenue, notamment en présence d’échantillons de taille relativement faible. Dans le cas où la valeur du coefficient de corrélation de Pearson serait très influencée par une valeur, il pourrait être une bonne pratique de calculer la valeur du coefficient de corrélation de Pearson avec et sans cette valeur afin de pouvoir quantifier son influence sur la relation étudiée (Halperin, 1986). Une alternative pourrait être aussi d’étudier la relation à l’aide d’autres types de coefficients que celui de Pearson, tels que celui de Spearman, présenté plus bas. Cet exemple doit faire prendre conscience qu’il n’est pas toujours pertinent de calculer le coefficient de corrélation de Pearson. En ce sens, lorsqu’on cherche à inférer la valeur du coefficient de corrélation de Pearson dans la population étudiée, il convient de vérifier certains prérequis, lesquels sont abordés plus loin dans ce livre.

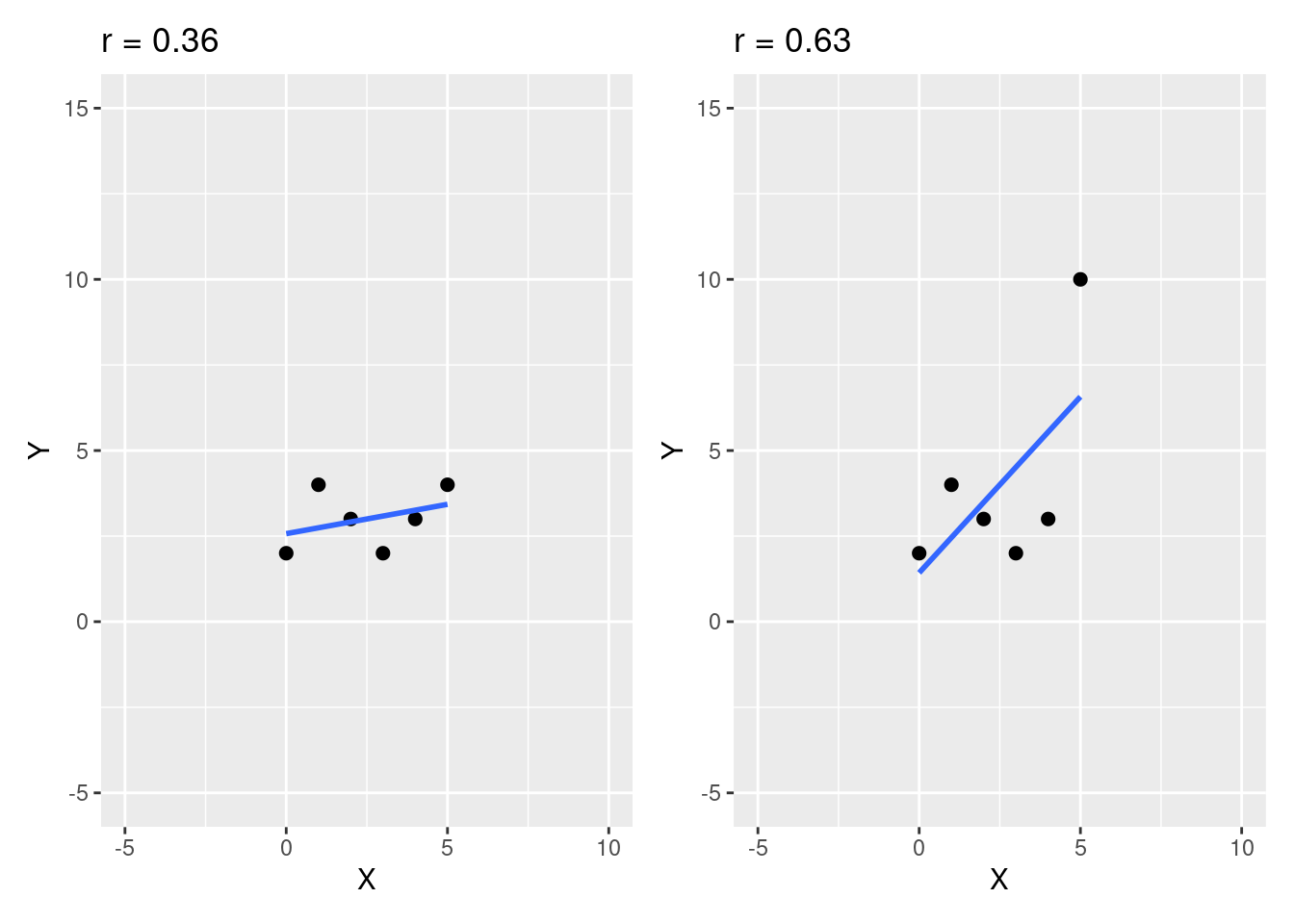
Influence d'une valeur extrême sur la valeur du coefficient de corrélation de Pearson en présence d'un petit échantillon

Figure 4.7: Influence d’une valeur extrême sur la valeur du coefficient de corrélation de Pearson en présence d’un petit échantillon

Lorsque la relation étudiée ne semble pas linéaire mais s’apparente assez clairement à d’autres fonctions mathématiques, telles que des relations logarithmiques ou polynomiales, il est possible de transformer une des variables, voire les deux, pour rendre la relation linéaire et à nouveau étudiable à l’aide du coefficient de corrélation de Pearson (Halperin, 1986). Toutefois, il est aussi possible de créer des modèles de régression non linéaires afin de regarder si ces modèles correspondent bien aux données. La détermination et la validation d’un modèle non linéaire qui correspondrait bien aux données confirmerait alors que la relation étudiée a une forme particulière et potentiellement prédictible. Les procédures pour explorer différents modèles de régression (linéaires et non linéaires) sont abordées au chapitre suivant. Enfin, une dernière alternative possible, pour étudier la relation entre deux variables quantitatives dont les distributions ne permettraient pas d’utiliser correctement le coefficient de corrélation de Pearson, serait l’utilisation de coefficients de corrélation basés sur les rangs, tels que le coefficient de corrélation de Spearman.

Le coefficient de corrélation de Spearman

Lorsque le coefficient de corrélation de Pearson ne permet pas de caractériser fiablement le degré de relation linéaire entre les valeurs de deux variables (e.g., en présence de valeurs aberrantes au sein d’un échantillon de petite taille), une alternative peut être d’étudier le degré de relation linéaire entre les rangs de ces deux variables. Le rang, c’est le classement (ou la position) d’une observation donnée au sein d’une variable en fonction de sa valeur. Dans une variable, les observations avec les valeurs les plus faibles seront associées aux rangs les plus bas alors que les observations avec les valeurs les plus élevées seront associées aux rangs les plus élevés. Une illustration de la notion de rang est proposée dans le Tableau ?? pour la variable hp du jeu de données mtcars. Dans ce tableau, les lignes ont été ordonnées sur la base des rangs de la variable hp. On pourra remarquer que dans le tableau, nous avons ce qu’on appelle des ex-aequos, c’est-à-dire que plusieurs observations peuvent présenter les mêmes valeurs, et donc avoir le même rang.

``` ```{=html}
(\#tab:tableranks)Rangs de la variable hp du jeu de données mtcars

hp (valeur)

hp (rang)

52

1.0

62

2.0

65

3.0

66

4.5

66

4.5

91

6.0

93

7.0

95

8.0

97

9.0

105

10.0

109

11.0

110

13.0

110

13.0

110

13.0

113

15.0

123

16.5

123

16.5

150

18.5

150

18.5

175

21.0

175

21.0

175

21.0

180

24.0

180

24.0

180

24.0

205

26.0

215

27.0

230

28.0

245

29.5

245

29.5

264

31.0

335

32.0

Le fait d’étudier l’existence d’une relation linéaire entre les rangs et non plus entre les valeurs de deux variables permet de s’affranchir de l’influence possible de valeurs très extrêmes, dans l’une et/ou l’autre variable, sur le calcul final de la corrélation. Pour déterminer alors la valeur de la corrélation, une manière de procéder est d’appliquer la méthode de calcul du coefficient de corrélation de Pearson en utilisant non plus les valeurs des variables, mais les rangs correspondants. Cette methode, c’est celle du calcul du coefficient de corrélation de Spearman (rho). Si l’on suit stricto sensu cette définition, nous pourrions alors utiliser le code suivant pour avoir le coefficient de corrélation de Spearman :

cor(x = rank(mtcars$hp), y = rank(mtcars$mpg), method = "pearson")
## [1] -0.8946646

Toutefois, il existe une manière plus directe d’écrire les choses avec la fonction cor, qui contient un argument spécifiquement dédié au calcul du coefficient rho de Spearman :

cor(x = mtcars$hp, y = mtcars$mpg, method = "spearman")
## [1] -0.8946646

La fonction cor.test permet aussi de calculer le coefficient de corrélation de Spearman en fournissant aussi des informations potentiellement intéressantes pour donner une idée de la significativité statistique de l’estimation de rho dans la population étudiée.

cor.test(x = mtcars$hp, y = mtcars$mpg, method = "spearman")
## 
##  Spearman's rank correlation rho
## 
## data:  mtcars$hp and mtcars$mpg
## S = 10337, p-value = 5.086e-12
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##        rho 
## -0.8946646

Si l’on veut produire une représentation graphique qui illustre la valeur de rho, il pourrait être davantage pertinent de non plus montrer un nuage de points à partir des valeurs des variables mises en lien, mais un nuage de points à partir de leurs rangs respectifs (cf. code ci-dessous et Figure 4.8).

mtcars %>%
  mutate(hp_rank = rank(hp), mpg_rank = rank(mpg)) %>%
  ggplot(aes(x = hp_rank, y = mpg_rank)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)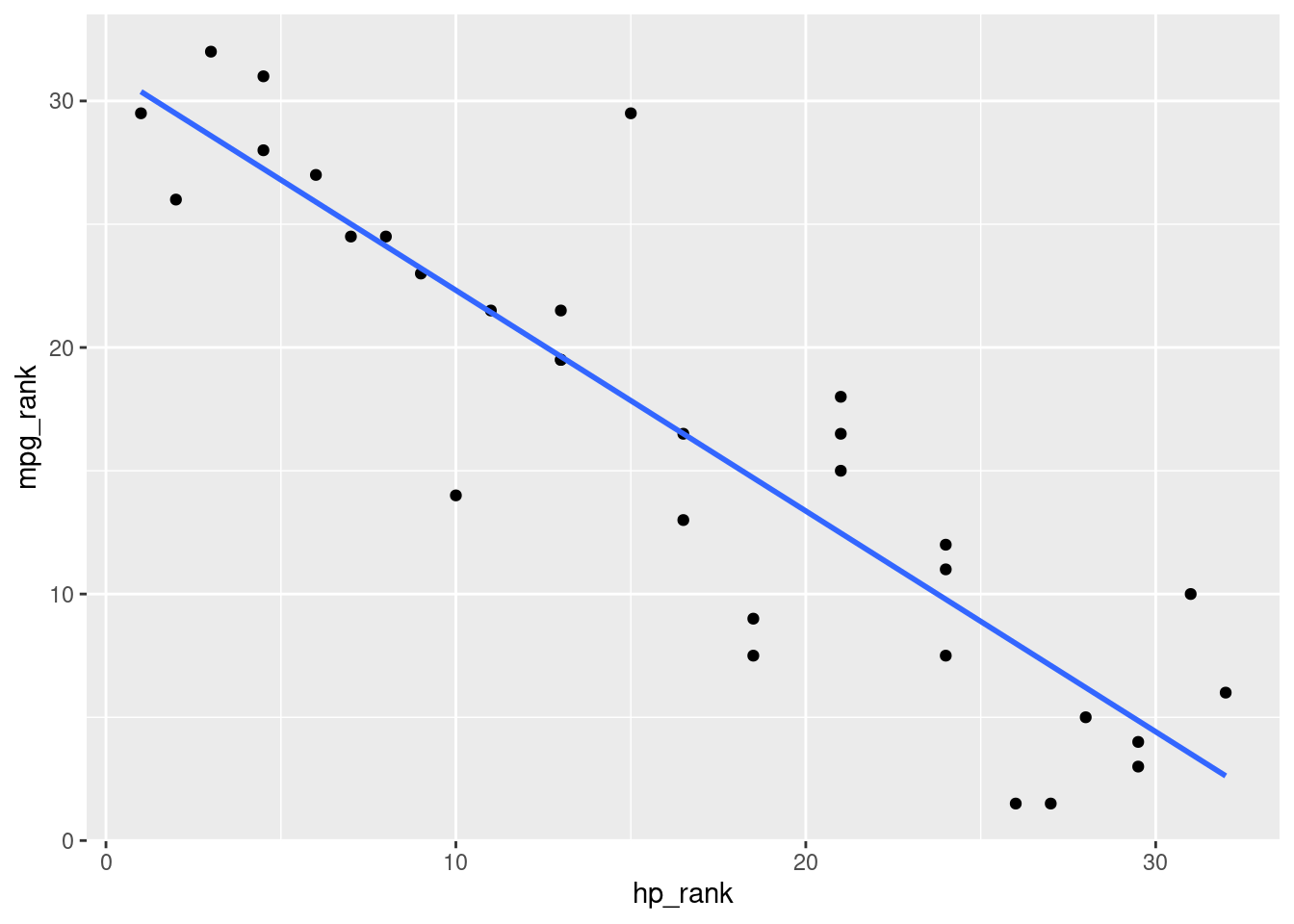
Graphique pour le coefficient de corrélation de Spearman

Figure 4.8: Graphique pour le coefficient de corrélation de Spearman

En matière d’interprétation, des valeurs de rho positives indiqueront que les deux variables mises en lien tendent à augmenter simultanément, on parlera alors de relation monotone positive. Dans le cas inverse, des valeurs négatives indiqueront que les deux variables mises en lien tendent à diminuer simultanément, on parlera alors de relation monotone négative. À noter cependant que de par son calcul, la valeur de rho ne permet pas de renseigner sur la forme de relation qu’il pourrait y avoir entre les valeurs des deux variables (e.g., linéaire ou curvilinéaire par exemple). Ceci est illustré sur la Figure 4.9. Sur cette figure, le graphique de gauche montre la relation entre les valeurs des variables \(X\) et \(Y\), qui est caractérisée par un coefficient de corrélation de Spearman (rho) de 1, indiquant donc que la relation est parfaitement monotone positive, sans préjuger de la forme particulière que pourrait présenter la relation. Pour mieux comprendre pourquoi cette valeur de rho est de 1, le graphique de droite de la figure montre la relation entre les rangs de ces deux variables \(X\) et \(Y\). On voit que la relation entre les rangs est effectivement parfaitement linéaire.

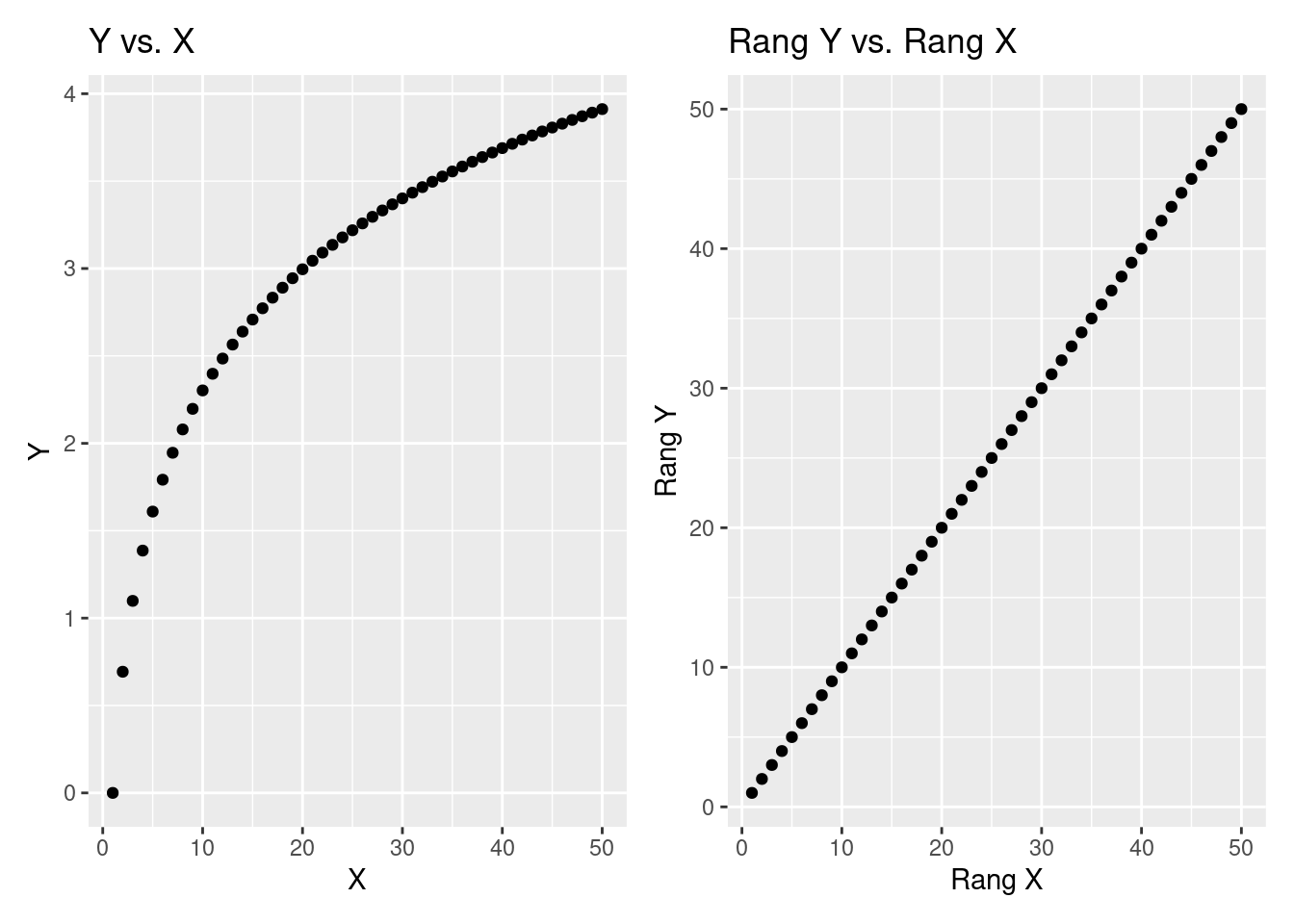
Distinction entre la relation observée entre les valeurs (graphique de gauche) et les rangs (graphique de droite) de deux variables

Figure 4.9: Distinction entre la relation observée entre les valeurs (graphique de gauche) et les rangs (graphique de droite) de deux variables

4.2 Relation entre deux variables qualitatives

4.2.1 Étudier graphiquement la relation

Plusieurs types de graphiques peuvent être envisagés lorsqu’il s’agit de visualiser des données relatives au croisement de deux variables qualitatives. Une première approche consiste à utiliser des graphiques avec barres mises côte-à-côte, comme illustré sur la Figure 4.10, qui a été réalisée à partir du jeu de données JointSports, lequel est utilisable après installation et chargement du package vcd. JointSports contient des données résumées d’effectifs mis en lien avec les modalités de différentes variables qualitatives, comme on aurait pu l’obtenir avec la fonction count() dans les derniers exemples du chapitre précédent. (La différence qu’il y a avec ces précédents exemples est qu’ici, l’effectif est désigné par la variable Freq, alors qu’il s’agissait de la variable n auparavant.) Pour information, JointSports contient les données d’une enquête s’étant intéressée, en 1983 et 1985, aux opinions d’étudiants danois de 16 à 19 ans sur la pratique sportive mixte.

library(vcd)

# Reconfiguration de l'ordre des modalités de la variable opinion, et calcul 
# des effectifs totaux pour les catégories étudiées

JointSports_new <- 
  JointSports %>%
  mutate(opinion = fct_relevel(opinion, 
                               "very bad", 
                               "bad", 
                               "indifferent", 
                               "good", 
                               "very good"),
         gender = fct_relevel(gender, "Girl", "Boy")) %>%
  group_by(gender, opinion) %>%
  summarize(Freq = sum(Freq))

# Création des graphiques
A <- 
  ggplot(data = JointSports_new, aes(x = gender, y = Freq, fill = opinion)) +
  geom_bar(stat = "identity",  position = "dodge") +
  scale_fill_brewer(palette = "Greens") +
  theme(legend.position = "right") +
  ggtitle("A : Mise en avant de la comparaison des opinions")

B <- 
  ggplot(data = JointSports_new, aes(x = opinion, y = Freq, fill = gender)) +
  geom_bar(stat = "identity",  position = "dodge") +
  theme(legend.position = "right") +  
  ggtitle("B : Mise en avant de la comparaison des genres")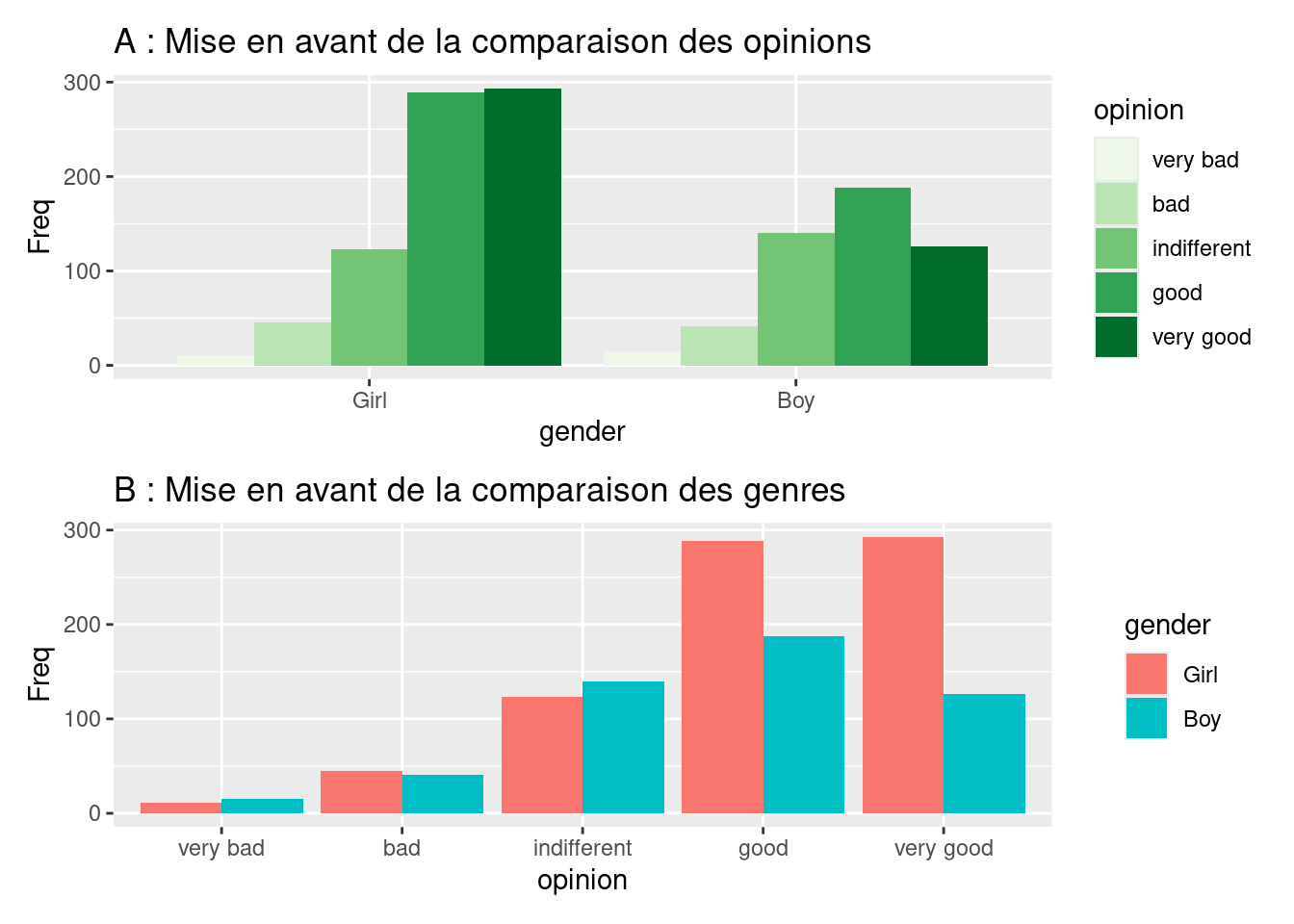
Exemples de diagramme en barres mises côte-à-côte

Figure 4.10: Exemples de diagramme en barres mises côte-à-côte

Pour pouvoir réaliser le graphique A de la Figure 4.10, il a fallu indiquer dans la fonction ggplot(), grâce à l’argument x =, la variable dont on voulait voir les modalités en abscisses, et il a fallu renseigner pour les ordonnées, à l’aide de l’argument y =, la variable contenant les effectifs correspondants, le tout toujours à l’intérieur de la fonction aes(). Étant donné que les données à montrer le long de l’axe des ordonnées sont explicitement indiquées avec Freq, il convient d’indiquer à l’intérieur de la fonction geom_bar() l’argument stat = "identity", ce qui contraint à déterminer la hauteur des barres en fonction des valeurs de la variable Freq. À l’intérieur de la fonction ggplot(), plus exactement au niveau de la fonction aes(), c’est l’argument fill = opinion qui a permis d’indiquer qu’on voulait des couleurs de remplissage différentes selon les modalités de la variable opinion. Enfin, c’est grâce à l’argument position = "dodge", à l’intérieur de la fonction geom_bar(), que l’on a pu obtenir des barres mises côte-à-côte, et non pas de manière empilée. Une logique similaire a été utilisée pour le graphique B en modifiant le code de telle sorte à ce que la distinction de l’information avec des couleurs différentes se fasse avec la variable gender, et non plus opinion.

Les graphiques A et B de la Figure 4.10 montrent l’importance de la configuration du graphique en fonction des comparaisons que l’on veut principalement faire, et donc du message que l’on veut prioritairement délivrer. Un principe qui peut guider la conception du graphique est le fait qu’il est plus facile de comparer des barres qui sont mises juste côte-à-côte. Sur la base de ce principe, le graphique A de la Figure 4.10 permet de comparer plus facilement les diverses opinions relevées pour les garçons d’un côté et pour les filles de l’autre, alors que le graphique B permet de comparer plus facilement les réponses provenant des deux genres et cela pour chaque type d’opinion. Comme indiqué par Wilke (2018), les types de graphiques illustrés avec les graphiques A et B de la Figure 4.10 peuvent parfois se voir attribuer le reproche que s’il est relativement facile de lire les informations encodées par des positions (cf. ligne de base sur les graphiques), il peut être être difficile de lire les informations encodées par une couleur dont la signification est indiquée en légende, car cela demande un effort mental supplémentaire de garder en tête la signification de la légende lorsqu’on lit le graphique. Pour palier ce problème, qui, selon Wilke (2018), est au final une affaire de goût, on pourrait utiliser la fonction facet_wrap() pour créer une figure telle que la Figure 4.11. Cette figure reprend la logique du graphique A de la Figure 4.10, avec un besoin de légende pour la variable opinion qui n’existe plus car la fonction facet_wrap() a permis de montrer les diagrammes en barres pour les deux genres de manière séparée, dans des encarts différents, et avec chacun leur propre axe des abscisses relatif aux modalités de la variable opinion.

ggplot(data = JointSports_new, aes(x = opinion, y = Freq)) +
  geom_bar(stat = "identity") +
  facet_wrap(. ~ gender)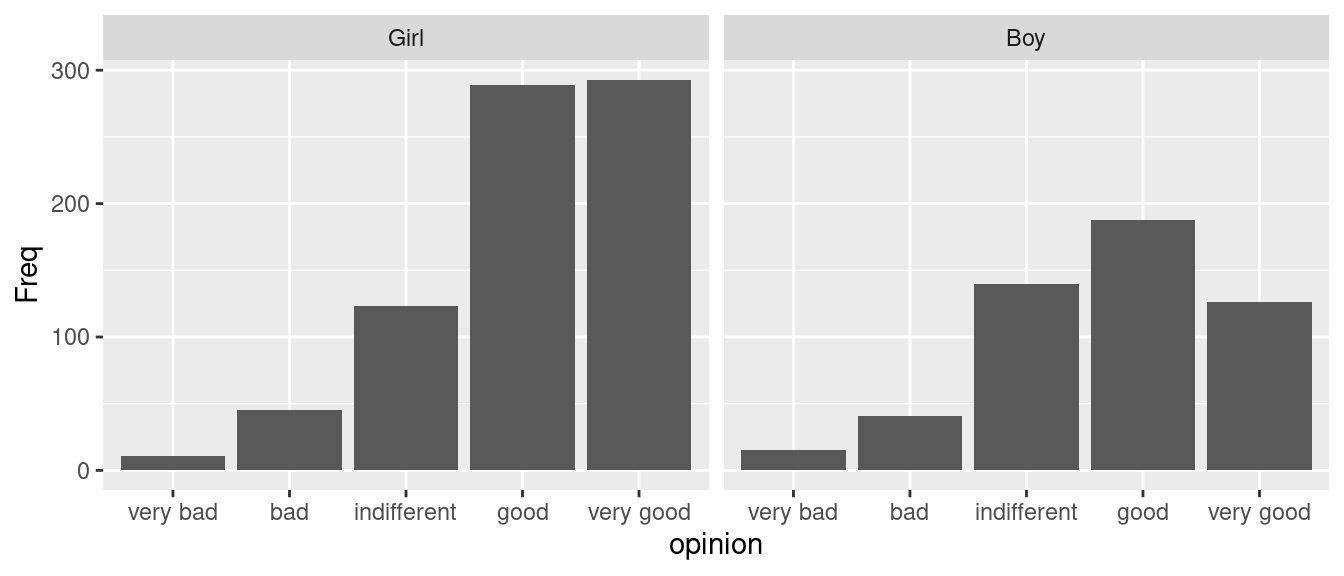
Diagrammes en barres côte-à-côte séparés selon une variable qualitative

Figure 4.11: Diagrammes en barres côte-à-côte séparés selon une variable qualitative

Dans certains cas, on peut vouloir comparer les effectifs relatifs aux modalités d’une première variable qualitative avec des barres mises côte-à-côte, et n’utiliser la seconde variable qualitative que pour avoir un peu d’éléments de contexte “à l’intérieur” des effectifs affichés pour la première variable qualitative. La Figure 4.12 illustre ce cas de figure où la hauteur des barres sert prioritairement à comparer les effectifs relatifs à diverses opinions, et la coloration des barres sert à fournir une idée de la répartition (hommes / femmes dans l’exemple) dans les réponses, sans pourtant avoir l’ambition de comparer cette répartition facilement d’un type d’opinion à un autre.

JointSports_new %>%
  ggplot(aes(x = opinion, y = Freq, fill = gender)) +
  geom_bar(stat = "identity") +
  geom_text(aes(label = Freq), size = 3, position = position_stack(vjust = 0.5))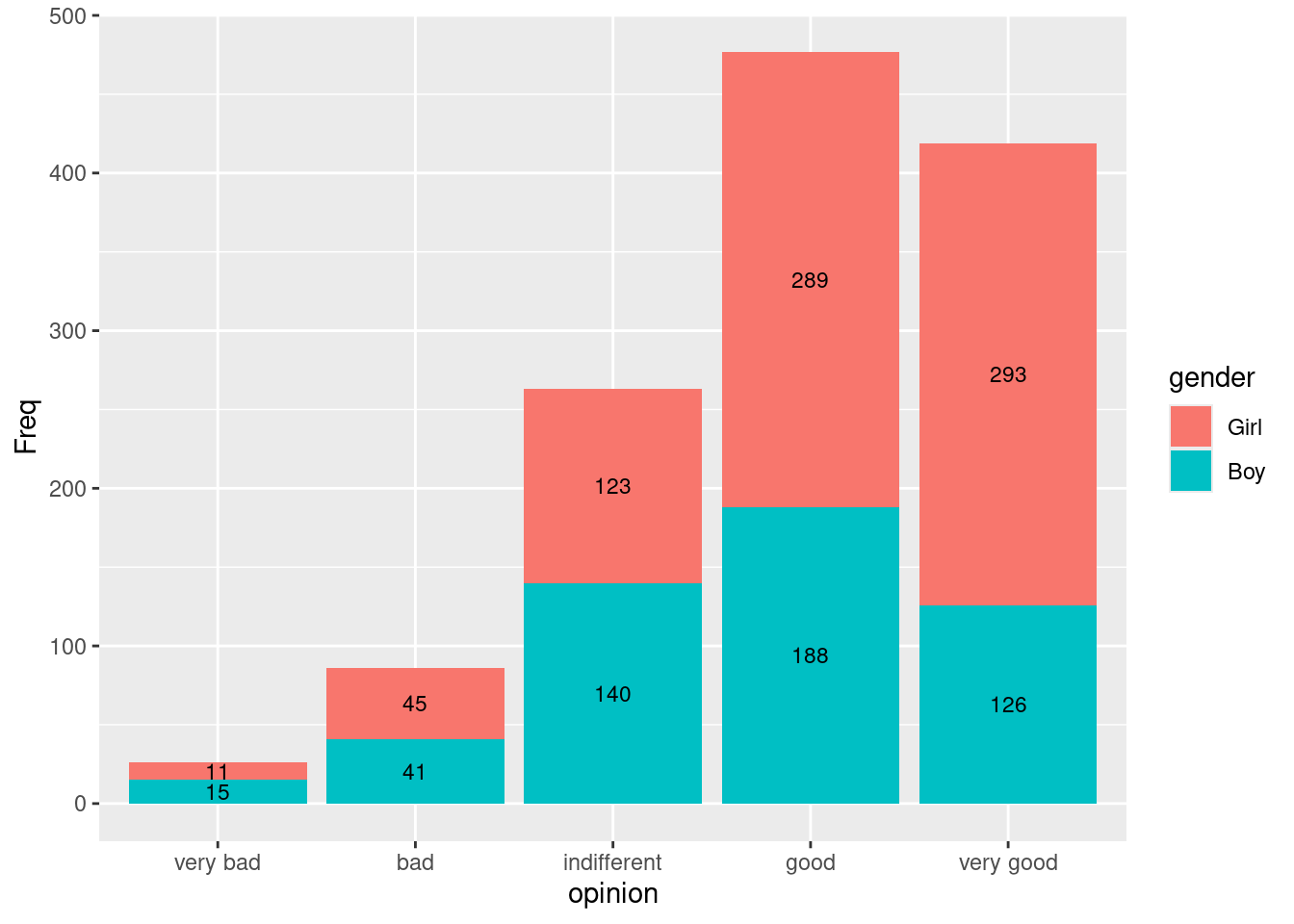
Exemple de diagramme en barres empilées

Figure 4.12: Exemple de diagramme en barres empilées

Les graphiques présentés dans cette sous-partie montrent des valeurs d’effectifs, mais selon l’objectif, il pourrait être aussi envisagé d’utiliser ces graphiques pour montrer des proportions. Cela dit, il existe d’autres visualisations possibles des proportions pour visualiser le lien entre deux variables qualitatives. Ces visualisations peuvent être consultées dans l’ouvrage en ligne de Wilke (2018).

4.2.2 Étudier numériquement la relation

Effectifs et proportions

Lorsqu’il s’agit de mener une étude numérique de la relation entre deux variables qualitatives, une première démarche à mettre en oeuvre est de récapituler numériquement les effectifs qui correspondent au croisement des deux variables. Pour cela, la fonction table() intégrée à R de base s’avère très pratique. Cependant, cette fonction requiert d’utiliser le jeu de données initial complet (i.e., avec toutes les observations), ce qui n’est pas le cas du jeu de données JointSports que nous avons utilisé précédemment, car ce dernier contient des effectifs déjà récapitulés par modalité de variable. Pour pouvoir illustrer le fonctionnement de la fonction table() avec les informations du jeu de données JointSports, j’ai donc crée un jeu de données complet qui, une fois résumé comme c’est le cas plus haut avec JointSports, donnerait les mêmes résultats. Ce nouveau jeu de données se nomme JointSports_full.

# Création du jeu de données JointSports_full

id <- rep(1 : sum(JointSports$Freq))
year <- c(rep("1983", 656), rep("1985", 615))
grade <- c(rep("1st", 350), rep("3rd", 306), rep("1st", 354), rep("3rd", 261))
gender <- c(rep("Boy", 134), rep("Girl", 216), rep("Boy", 115), 
            rep("Girl", 191),  rep("Boy", 157), rep("Girl", 197), 
            rep("Boy", 104), rep("Girl", 157))
opinion <- c(
  rep("very good", 31), rep("good", 51), rep("indifferent", 38), 
  rep("bad", 10), rep("very bad", 4), 
  rep("very good", 103), rep("good", 67), rep("indifferent", 29), 
  rep("bad", 15), rep("very bad", 2), 
  rep("very good", 23), rep("good", 39), rep("indifferent", 36), 
  rep("bad", 15), rep("very bad", 2), 
  rep("very good", 61), rep("good", 72), rep("indifferent", 39), 
  rep("bad", 16), rep("very bad", 3), 
  rep("very good", 41), rep("good", 67), rep("indifferent", 35), 
  rep("bad", 12), rep("very bad", 2), 
  rep("very good", 77), rep("good", 80), rep("indifferent", 27), 
  rep("bad", 10), rep("very bad", 3), 
  rep("very good", 31), rep("good", 31), rep("indifferent", 31), 
  rep("bad", 4), rep("very bad", 7), 
  rep("very good", 52), rep("good", 70), rep("indifferent", 28), 
  rep("bad", 4), rep("very bad", 3)
  )

JointSports_full <- 
  data.frame(id = id, 
             year = year, 
             grade = grade, 
             gender = gender, 
             opinion = opinion) %>%
  mutate(opinion = fct_relevel(opinion, 
                               "very bad", 
                               "bad", 
                               "indifferent", 
                               "good", 
                               "very good"))

Une fois que l’on a un jeu de données complet sous la main, il est possible de créer ce qu’on appelle un tableau de contingence, c’est-à-dire ici un tableau qui récapitule numériquement les effectifs à la croisée des deux variables qui nous intéressent. Pour faire cela, on peut utiliser la fonction table() en suivant différentes méthodes montrées ci-dessous. (Le code montré ci-dessous aboutit aux mêmes informations que celles montrées sur la Figure 4.12 ci-dessus.)

# 1ère méthode
tab <- 
  with(JointSports_full,
       table(opinion, gender))

# 2ème méthode
tab <- table(JointSports_full$opinion, JointSports_full$gender)

# Visualisation du tableau de contingence
tab
##              
##               Boy Girl
##   very bad     15   11
##   bad          41   45
##   indifferent 140  123
##   good        188  289
##   very good   126  293

Un tableau de contingence permet donc de comparer des effectifs en fonction de plusieurs modalités et variables à la fois. Le problème, lorsqu’on utilise des effectifs, est que certaines comparaisons peuvent être difficiles à faire lorsque les effectifs totaux liés aux différentes modalités ne sont pas comparables. Par exemple, dans le résultat montré ci-dessus, l’effectif total des filles est de 761 alors que celui des garçons est de 510, ce qui rend difficile la comparaison des garçons et des filles pour les différents types d’opinion recensés dans l’enquête danoise présentée plus haut. C’est pour cela qu’il convient, dans certains cas, de calculer les proportions correspondant à ces différents effectifs. Pour ce faire, on peut :

  • Utiliser la fonction prop.table(), qui va convertir en proportions les effectifs montrés plus haut en considérant l’effectif total de tout le tableau :
round(prop.table(tab) * 100, digits = 2)
##              
##                 Boy  Girl
##   very bad     1.18  0.87
##   bad          3.23  3.54
##   indifferent 11.01  9.68
##   good        14.79 22.74
##   very good    9.91 23.05
  • Utiliser la fonction lprop() du package questionr, qui va convertir en proportions les effectifs montrés plus haut en considérant l’effectif total de chaque ligne du tableau :
##              
##               Boy   Girl  Total
##   very bad     57.7  42.3 100.0
##   bad          47.7  52.3 100.0
##   indifferent  53.2  46.8 100.0
##   good         39.4  60.6 100.0
##   very good    30.1  69.9 100.0
##   All          40.1  59.9 100.0
  • Utiliser la fonction cprop() du package questionr, qui va convertir en proportions les effectifs montrés plus haut en considérant l’effectif total de chaque colonne du tableau :
##              
##               Boy   Girl  All  
##   very bad      2.9   1.4   2.0
##   bad           8.0   5.9   6.8
##   indifferent  27.5  16.2  20.7
##   good         36.9  38.0  37.5
##   very good    24.7  38.5  33.0
##   Total       100.0 100.0 100.0

Il convient de noter que les proportions données par ces différentes fonctions doivent être utilisées selon les comparaisons que l’on veut faire. L’analyse descriptive consiste alors à voir si, tant d’un point de vue graphique que numérique, on observe des différences de scores particulières entre les modalités d’une variable qualitative en fonction des modalités de l’autre variable qualitative. Si l’on considère le dernier tableau de résultats ci-dessus, on peut par exemple observer une très légère tendance à ce que les garçons soient davantage polarisés, par rapport aux filles, sur des opinions négatives vis-à-vis des pratiques sportives mixtes, alors que les filles seraient légèrement plus polarisées que les garçons sur des opinions positives, ce qui n’empêche pas que, pour les deux genres, il y a une polarisation principale sur des opinions neutres à positives.

Si les proportions permettent en principe de mieux comparer les effectifs de sous-groupes (e.g., les opinions par groupe de genre dans l’exemple ci-dessus) lorsque les effectifs des groupes parents sont de tailles différentes (comme c’est le cas pour les groupes de genre dans l’exemple ci-dessus), il convient tout de même de faire attention aux conclusions que l’on tire lorsqu’on s’en tient à une analyse globale, car ces conclusions dépendent de la manière dont les individus des groupes parents sont répartis dans chacun des sous-groupes. Un exemple connu qui permet d’illustrer cette vigilance à avoir lorsqu’on étudie le croisement de variables qualitatives est le cas du taux de réussite des femmes à l’université de Berkeley en 1973, qui apparaissait bien inférieur à celui des hommes lorsqu’on considérait les taux de réussite par genre à l’échelle de l’ensemble de l’université (Bickel et al., 1975), avec 30.3 % de réussite chez les femmes contre 44.5 % de réussite chez les hommes (cf. Figure 4.13).

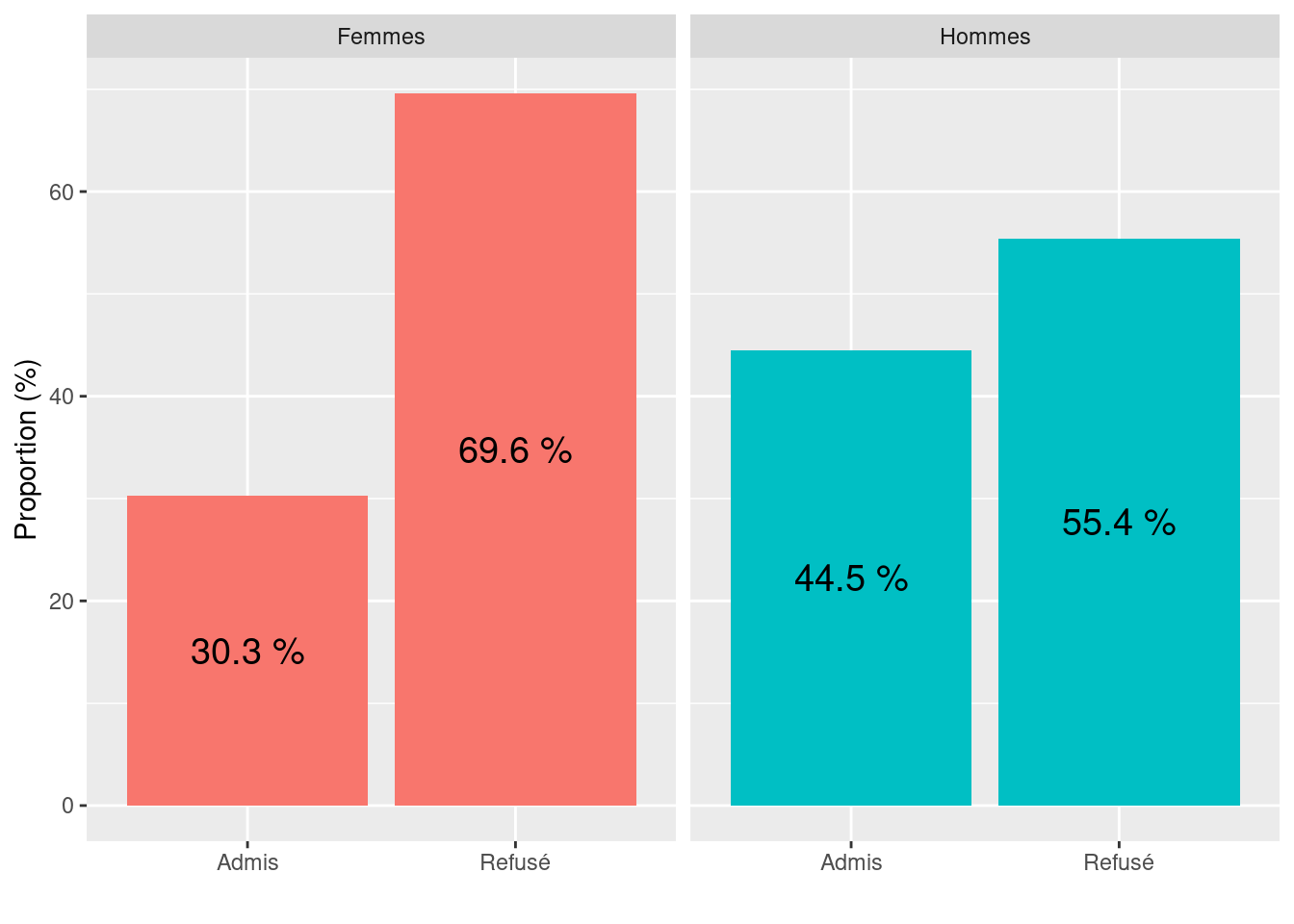
Taux de réussite des étudiants femmes et hommes à l'Université de Berkeley en 1973, approche globale (Bickel et al., 1975)

Figure 4.13: Taux de réussite des étudiants femmes et hommes à l’Université de Berkeley en 1973, approche globale (Bickel et al., 1975)

Toutefois, une analyse par département permettait de voir que les taux de réussite des femmes étaient en réalité supérieurs voire nettement supérieurs à ceux des hommes dans la plupart des départements (cf. Figure 4.14).

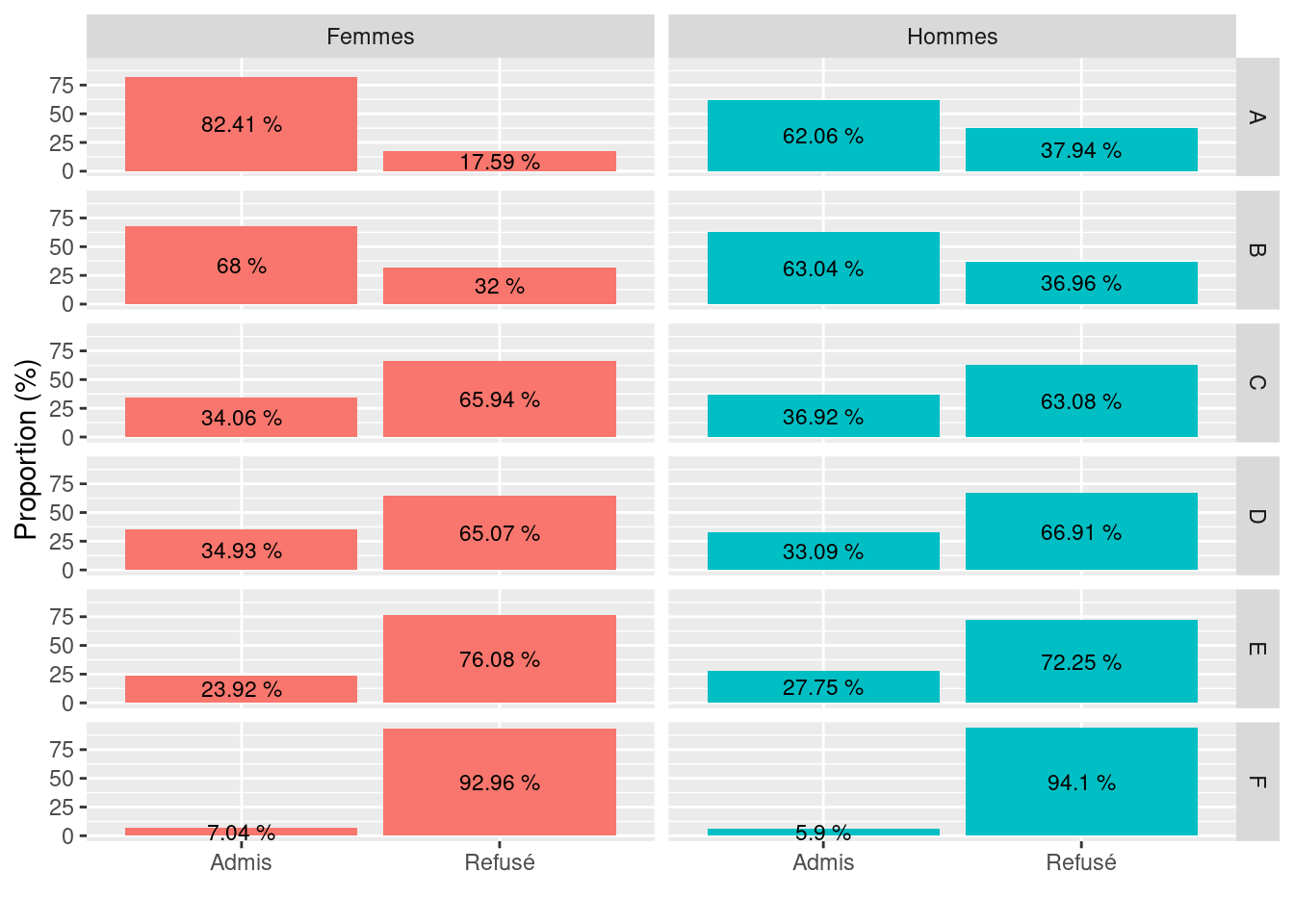
Taux de réussite des étudiants femmes et hommes à l'Université de Berkeley en 1973, approche par département (Bickel et al., 1975)

Figure 4.14: Taux de réussite des étudiants femmes et hommes à l’Université de Berkeley en 1973, approche par département (Bickel et al., 1975)

Cette situation, qui peut paraître étonnante, illustre à nouveau ce qu’on appelle un paradoxe de Simpson. Dans le cas présent, l’apparent paradoxe s’explique par le fait que les femmes avaient en proportion davantage candidaté que les hommes dans des départements où le taux de réussite global était moins bon. Ceci est illustré sur la Figure 4.15.

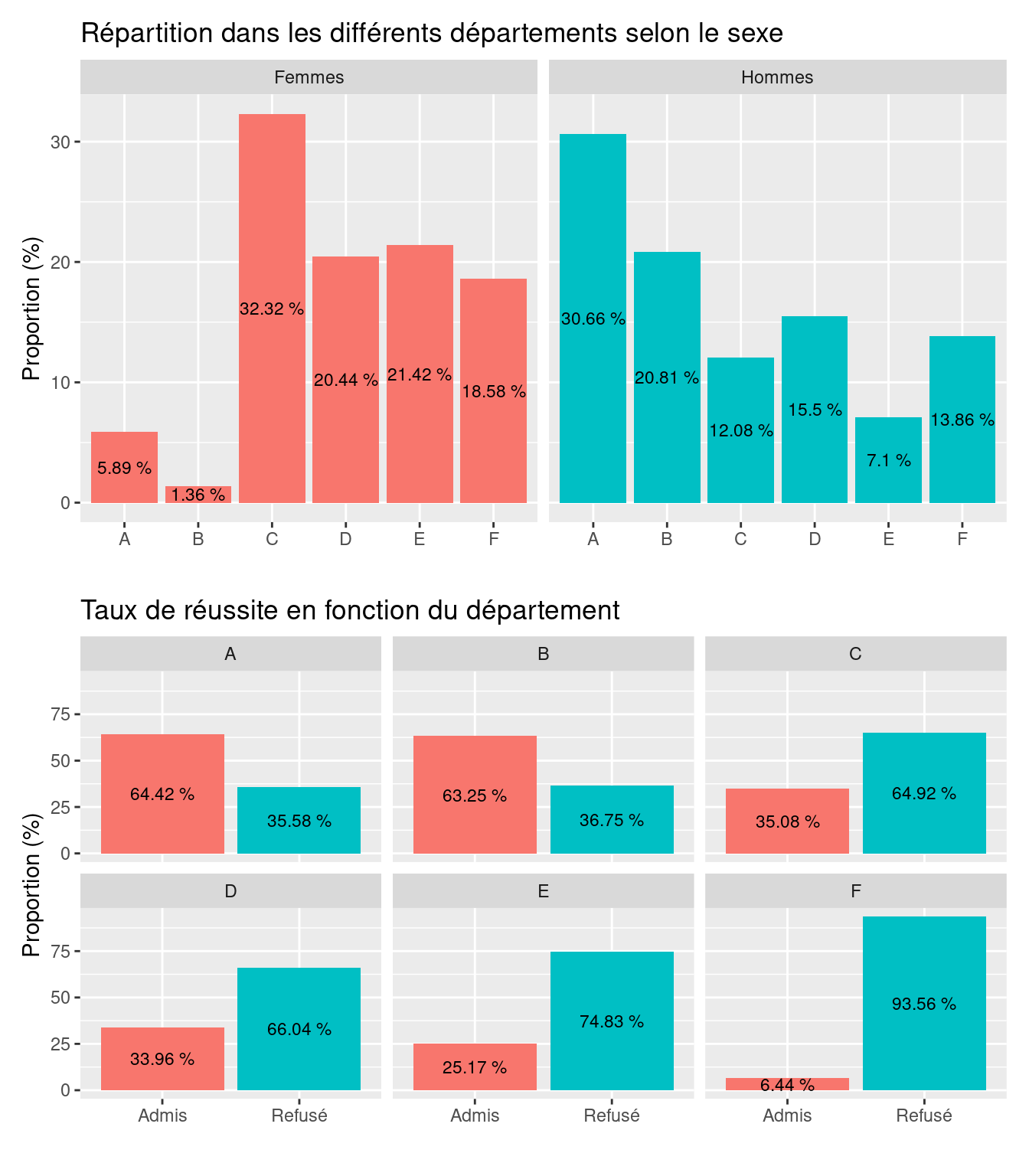
Mise en avant du département d'inscription comme facteur confondant dans l'étude du lien entre le genre et le taux de réussite à l'Université de Berkeley en 1973 (Bickel et al., 1975)

Figure 4.15: Mise en avant du département d’inscription comme facteur confondant dans l’étude du lien entre le genre et le taux de réussite à l’Université de Berkeley en 1973 (Bickel et al., 1975)

Autrement dit, les hommes se retrouvaient avec un pourcentage de réussite global bien meilleur que celui des femmes seulement parce que, comparativement aux femmes, les hommes s’étaient en proportion davantage engagés dans les départements où les taux de réussite étaient bien meilleurs.

Au-delà du tableau de contingence, plusieurs outils statistiques sont disponibles pour quantifier le lien entre les modalités de deux variables qualitatives (Jané et al., 2023). On s’intéresse ici plus spécifiquement au coefficient Phi (\(\Phi\)), au \(V\) de Cramer, à la différence de risque, au risque relatif, et au rapport des cotes. À noter que tous ces indices statistiques, excepté le \(V\) de Cramer, sont essentiellement faits pour analyser le lien entre deux variables qualitatives dont l’une ne présenterait que deux modalités (on parle alors de variable binaire).

Coefficient Phi

Le coefficient \(\Phi\) est une valeur qui peut être comprise entre -1 et 1 (ou entre 0 et 1 selon les manières de l’obtenir) et indique la force de la relation entre deux variables qualitatives binaires. Toutefois, seule la valeur absolue (entre 0 et 1 donc) est à interpréter. Le signe (si jamais différents signes peuvent apparaître selon le calcul utilisé) ne fait que renseigner sur la diagonale du tableau de contingence où les individus sont davantage polarisés. Pour comprendre comment \(\Phi\) peut être calculé, prenons les tableaux de contingence montrés ci-dessous (Figure 4.16) :

Tableaux de contingence schématiques pour comprendre le calcul de Phi

Figure 4.16: Tableaux de contingence schématiques pour comprendre le calcul de Phi

On note sur ces tableaux qu’une valeur absolue de \(\Phi\) élevée sera attendue dans le cas où il y aura relativement beaucoup d’individus dans une diagonale et relativement peu d’individus dans l’autre diagonale (cf. tableaux du milieu et de droite ci-dessus). Si l’on prend comme base l’un des tableaux de contingence montrés ci-dessus, la formule du coefficient \(\Phi\) est la suivante (Jané et al., 2023) :

\[\Phi = \frac{(n_{11} \cdot n_{22}) - (n_{21} \cdot n_{12})}{\sqrt{(n_{11} + n_{21}) \cdot (n_{12} + n_{22}) \cdot (n_{11} + n_{12}) \cdot (n_{21} + n_{22})}}\] Une autre formule pour calculer \(\Phi\) (donnant systématiquement la valeur absolue du coefficient) pourrait être aussi la suivante (Jané et al., 2023) :

\[\Phi = \sqrt{\frac{\chi^2}{n}},\]

avec \(\chi^2\) la statistique “chi-carré” et \(n\) le nombre total d’individus. Pour calculer \(\Phi\) dans R, on peut utiliser la fonction phi() du package effectsize :

tab <- table(mtcars$am, mtcars$vs)
effectsize::phi(tab)
## Phi (adj.) |       95% CI
## -------------------------
## 0.00       | [0.00, 1.00]
## 
## - One-sided CIs: upper bound fixed at [1.00].

\(V\) de Cramer

Le \(V\) de Cramer est la forme généralisée de la force d’association entre deux variables qualitatives. Il peut donc être calculé à partir d’un tableau de contingence de n’importe quelle taille, prendre des valeurs absolues entre 0 et 1, et est ainsi l’équivalent du coefficient \(\Phi\) dans le cas d’un tableau de contingence 2 x 2 (2 variables qualitatives x 2 modalités chacune). La formule du \(V\) de Cramer est la suivante (Jané et al., 2023) :

\[V = \sqrt{\frac{\chi^2}{n \cdot (k-1)}},\] avec \(\chi^2\) la statistique « chi-carré », \(n\) le nombre total d’individus, et \(k\) le nombre de modalités de la variable qui a le moins de modalités. Pour calculer le \(V\) de Cramer dans R, on peut utiliser la fonction cramers_v() du package effectsize :

tab <- table(JointSports_full$gender, JointSports_full$opinion)
effectsize::cramers_v(tab)
## Cramer's V (adj.) |       95% CI
## --------------------------------
## 0.17              | [0.11, 1.00]
## 
## - One-sided CIs: upper bound fixed at [1.00].

Différence de risque

La différence de risque est une différence de proportions. La notion de risque peut ne pas être très pertinente pour certains contextes, mais elle l’est particulièrement dans un contexte de santé. Pour comprendre le calcul du risque puis de la différence de risque, regardons le tableau ci-dessous (Figure 4.17).

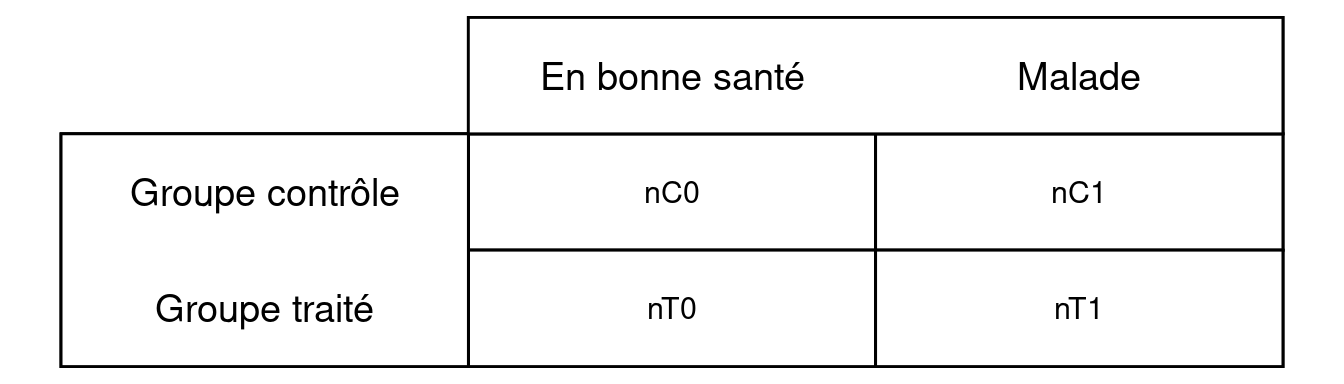
Tableau de contingence schématique pour comprendre le calcul des risques et des cotes

Figure 4.17: Tableau de contingence schématique pour comprendre le calcul des risques et des cotes

Dans le tableau ci-dessus, chaque case contenant un « n » est un effectif. Si l’on désire connaître le risque d’être malade dans le groupe contrôle (\(p_C\)) et dans le groupe traité (\(p_T\)), on fait les calculs suivants :

\[p_C = \frac{n_{C1}}{n_{C0} + n_{C1}}\]

\[p_T = \frac{n_{T1}}{n_{T0} + n_{T1}}\]

La différence de risque d’être malade pour le groupe contrôle par rapport au groupe traité de l’exemple, notée \(DR\), est alors :

\[p_C - p_T \] Avec R, la différence de risque peut être obtenue avec le package riskCommunicator. Pour utiliser le package riskCommunicator, il faut bien sûr ensuite le charger :

library(riskCommunicator)

Pour l’exemple, chargeons le jeu de données cvdd associé au package riskCommunicator:

data(cvdd)

Il s’agit d’un jeu de données avec plusieurs variables qualitatives, dont plusieurs sont plus précisément binaires (i.e., qui ne contiennent que deux modalités). Admettons que l’on souhaiterait connaître la différence de risque de mortalité cardiovasculaire (cvd_dh) sur une période de suivi donnée, cela en fonction de si l’on a développé une hypertension ou non (HYPERTEN). Pour cela, on peut utiliser la fonction gComp() du package riskCommunicator comme suit :

gComp(data = cvdd, X = "HYPERTEN", Y = "cvd_dth", outcome.type = "binary")
## Formula: 
## cvd_dth ~ HYPERTEN 
## 
## Parameter estimates: 
##                             HYPERTEN1_v._HYPERTEN0 Estimate (95% CI)
## Risk Difference                                 0.132 (0.098, 0.159)
## Risk Ratio                                      1.411 (1.275, 1.527)
## Odds Ratio                                      1.753 (1.505, 1.977)
## Number needed to treat/harm                                    7.559

Dans le résultat obtenu, la différence de risque est de 0.132, soit 13.2 %. À ce stade, il est fondamental de comprendre que le résultat obtenu dépend de la manière dont les modalités sont ordonnées dans les variables de type facteur utilisées pour faire les calculs. Regardons comment les modalités sont organisées pour les variables qui nous concernent :

levels(cvdd$HYPERTEN)
## [1] "0" "1"
levels(cvdd$cvd_dth)
## [1] "0" "1"

On remarque qu’à chaque fois, “0” est la première modalité, et “1” est la seconde modalité. C’est important de le savoir pour interpréter le résultat ensuite car la fonction gComp() calcule par défaut la différence de risque en faisant le risque de présenter la modalité 2 de la variable Y quand on a la modalité 2 de la variable X (ici le risque de mourir quand on est hypertendu) moins le risque de présenter la modalité 2 de la variable Y quand on a la modalité 1 de la variable X (ici le risque de mourir quand on n’est pas hypertendu). On peut d’ailleurs vérifier le calcul manuellement :

# Obtention d'un tableau de contingence avec proportions
tab <- table(cvdd$HYPERTEN, cvdd$cvd_dth)
risks <- questionr::lprop(tab)
colnames(risks) <- c("vivant", "mort", "total")
rownames(risks) <- c("non-hypertendu", "hypertendu", "total")
risks
##                 
##                  vivant mort  total
##   non-hypertendu  67.8   32.2 100.0
##   hypertendu      54.6   45.4 100.0
##   total           58.2   41.8 100.0
# Calcul de la différence de risque de mortalité 
# chez les hypertendus vs non-hypertendus (en %)
45.4-32.2
## [1] 13.2

Risque relatif

Le risque relatif, noté \(RR\), reprend les mêmes informations que celles utilisées pour la différence de risque (\({p_T}\) et \({p_C}\)). La différence est qu’il ne s’agit plus d’une différence, mais d’un rapport entre les risques présentés par les groupes comparés. Sa formule pour comparer le groupe contrôle au groupe traité dans notre exemple débuté plus haut est la suivante :

\[RR = \frac{{p_C}}{{p_T}}\] Avec R, le risque relatif peut être obtenu avec le package riskCommunicator tel que montré pour le calcul de la différence de risque, en faisant toujours bien attention à quel risque est divisé par quel risque selon l’analyse qui est réellement souhaitée. Dans notre exemple débuté plus haut, il s’agit du même calcul que pour la différence de risque sauf qu’il ne s’agit plus d’un signe moins mais d’une division. Les résultats obtenus plus haut avec l’exemple de la différence de risque montrent aussi le risque relatif, qui est tel que le risque de mourir chez les hypertendus est 1.41 fois plus élevé que chez les non-hypertendus.

Rapports des cotes

Le rapport des cotes, noté \(OR\) pour Odds ratio en anglais, est une statistique dont le calcul peut à nouveau se comprendre à l’aide d’un tableau de contingence. Si l’on reprend le tableau de la Figure 4.17, on peut dire que la cote pour le fait d’être en bonne santé versus être malade dans le groupe contrôle est \(n_{C0}\)/\(n_{C1}\) et la cote pour le fait d’être en bonne santé versus malade dans le groupe traité est \(n_{T0}\)/\(n_{T1}\). Le rapport des cotes pour le groupe contrôle versus le groupe traité dans ce cas-là peut se calculer comme ceci :

\[ OR= \frac{n_{C0} / n{_{C1}}}{n_{T0} / n{_{T1}}}\]

Le rapport des cotes est toujours ≥0. Une valeur en-dessous de 1 signifie « moins de chances/risques », une valeur de 1 signifie « chances/risques équivalent(e)s », et une valeur au-dessus de 1 signifie « plus de chances ou de risques ». Le chiffre obtenu renseigne toujours sur un niveau de chances pour le groupe au numérateur par rapport au niveau de chances concernant le groupe au dénominateur (cf. formule ci-dessus). Avec R, le rapport des cotes peut être obtenu avec le package riskCommunicator tel que montré pour le calcul de la différence de risque, en faisant cette fois attention à quelle cote est divisée par quelle cote selon l’analyse qui est réellement souhaitée. Dans notre exemple débuté plus haut, le rapport des cotes est de 1.75. Cela signifie ici que la cote pour le fait de mourir (versus le fait de vivre) est 1.75 fois plus élevée quand on est hypertendu que lorsqu’on ne l’est pas. Pour comprendre le calcul, on peut le refaire manuellement :

# Obtention d'un tableau de contingence avec effectifs
tab <- table(cvdd$HYPERTEN, cvdd$cvd_dth)
colnames(tab) <- c("vivant", "mort")
rownames(tab) <- c("non-hypertendu", "hypertendu")
tab
##                 
##                  vivant mort
##   non-hypertendu    781  371
##   hypertendu       1685 1403
# Calcul des cotes pour les "chances" de mourir selon le groupe d'appartenance
cote_hypertendus <- 1403/1685
cote_non_hypertendus <- 371/781

# Calcul du rapport des cotes
OR <- cote_hypertendus / cote_non_hypertendus
OR
## [1] 1.75281

4.3 Relation entre une variable quantitative et une variable qualitative

Lorsqu’on analyse une variable quantitative en fonction d’une variable qualitative, on peut avoir des données quantitatives qui sont non appariées (étude de type between-subject design en anglais) ou appariées (étude de type within-subject design en anglais). Avoir des données non appariées signifie que les données quantitatives correspondant aux différentes modalités de la variable qualitative étudiée ne sont pas liées. Un exemple simple, pour ce premier cas, peut être l’analyse de la taille des individus en fonction du sexe. Dans ce cas, les données quantitatives de taille pour les personnes de sexe masculin, de sexe féminin, et de sexe indéterminé, proviendront forcément d’individus différents et ne formeront donc pas des paires. S’agissant des cas de données appariées, ils se retrouvent dans les études où plusieurs individus sont évalués plusieurs fois dans des conditions similaires ou différentes et que l’on cherche à comparer. En sciences du sport, un exemple relativement classique est de tester la performance d’endurance (variable quantitative) en ayant pris (condition de test) ou non (condition contrôle) une substance potentiellement ergonénique, la prise de substance ou non étant les modalités d’une même variable qualitative de type condition. Dans ce cas là, tous les individus auront des données dans les deux conditions et ces données seront donc appariées (dépendantes).

Étant donné que les contraintes graphiques et les statistiques à calculer diffèrent selon que l’on est en présence de (i) deux groupes (1 variable quantitative x 1 variable qualitative avec 2 modalités) ou (ii) trois groupes et plus (1 variable quantitative x 1 variable qualitative avec 3 modalités ou plus), les procédures graphiques et calculatoires présentées ci-après sont distinguées selon ces deux grands cas de figure.

4.3.1 Comparaison de deux groupes de données

4.3.1.1 Étudier graphiquement la relation

Lorsque l’on cherche à explorer la relation qu’il peut y avoir entre une variable quantitative et une variable qualitative, il peut être intéressant de visualiser la distribution de la variable quantitative en fonction de chaque modalité de la variable qualitative. Pour faire cela, il a été proposé dans la littérature d’user de graphiques appelés raincloud plots qui combinent les avantages de plusieurs techniques graphiques et statistiques et par là même pallient les manques ou défauts inhérents à chacune de ces techniques (Allen et al., 2019). Les blocs de code ci-dessous, et les Figures 4.18 et 4.19, proposent plusieurs options de mise en oeuvre de ce type de graphiques selon la situation d’étude (avec données non appariées et appariées).

Données non appariées

La Figure 4.18, qui est associée au bloc de code ci-dessous, montre un graphique approprié pour des données non appariées.

# Configuration du jeu de données pour l'exemple avec données non appariées.
# Il s'agit ici d'obtenir le jeu de données `iris` avec seulement deux modalités  
# de la variable `Species`, cela en enlevant la modalité `virginica`.
iris_two_species <-
  iris %>% filter(Species != "virginica")
ggplot(data = iris_two_species, aes(x = Species, y = Sepal.Length)) +
  geom_rain(point.args = rlang::list2(alpha = 0.3)) +
  stat_summary(
    geom = "errorbar",
    fun.data = "mean_sdl",
    fun.args = list(mult = 1),
    size = 1.1, 
    width = 0.06
    ) + 
  stat_summary(
    geom = "point",
    fun = "mean", 
    size = 3
    )
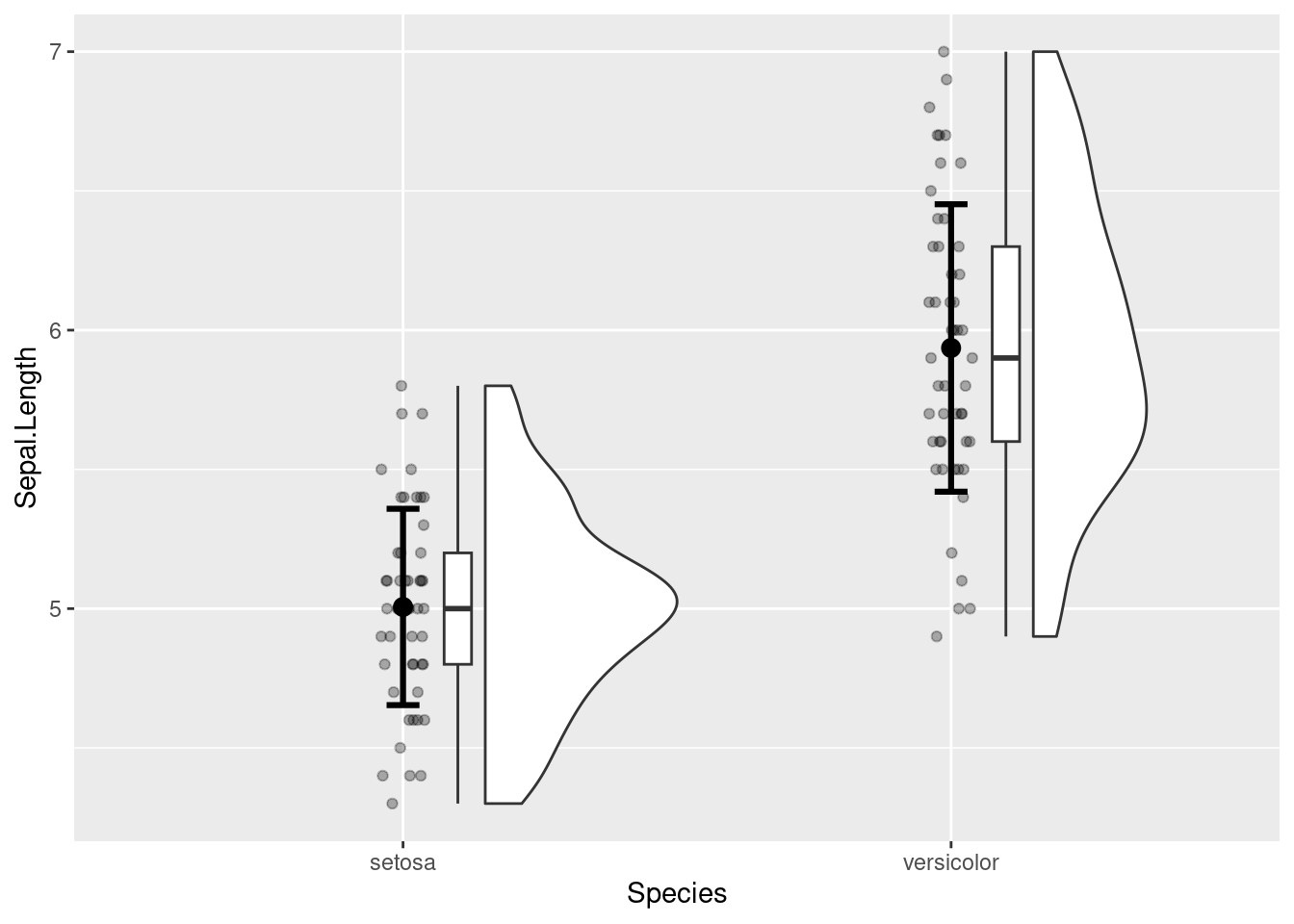
Exemple de graphique pour une comparaison de deux groupes de valeurs non-appariés (indépendants)

Figure 4.18: Exemple de graphique pour une comparaison de deux groupes de valeurs non-appariés (indépendants)

On note que pour montrer les moyennes et écarts-types sur la Figure 4.18, il a fallu utiliser la fonction stat_summary() du package Hmisc (qui est chargé automatiquement lors du chargement de ggplot2 après que Hmisc ait été installé). Cette fonction sert à visualiser un résumé statistique. Pour montrer les moyennes, on utilise fun = "mean", alors que pour montrer des écarts-types, on utilise fun.data = "mean_sdl". Pour les écarts-types, il faut ajouter fun.args = list(mult = 1) pour bien montrer une barre d’erreur ne correspondant qu’à un seul multiple de l’écart-type, car par défaut c’est deux fois l’écart-type qui est montré. On peut choisir la forme avec laquelle présenter le résumé statistique grâce à l’argument geom.

Données appariées

La Figure 4.19 montre une proposition de graphique dans le cas de l’étude d’une comparaison de deux groupes de données appariées. Pour cela, nous avons installé le package PairedData et chargé le jeu de données associé, appelé Blink. Pour information, Blink contient des données de taux de clignotement des yeux obtenues chez 12 sujets et dans deux conditions différentes : une tâche où il fallait diriger un stylo selon une trajectoire rectiligne (modalité Straight), et une tâche où il fallait diriger un stylo selon une trajectoire présentant des oscillations (Oscillating). Ce jeu de données a été un peu transformé pour pouvoir passer à l’étape de la conception graphique, comme montré ci-dessous.

# Charger le package
library(PairedData)

# Charger le jeu de données
data(Blink)

# Configurer le jeu de données pour l'exemple avec données appariées
Blink2 <-
  Blink %>%
  pivot_longer(cols = c(Straight, Oscillating), 
               names_to = "Condition", 
               values_to = "Blink_rate") %>%
  mutate(Condition = fct_relevel(Condition, "Straight", "Oscillating"))
ggplot(data = Blink2, aes(x = Condition, y = Blink_rate)) +
  geom_rain(
    rain.side = "f1x1",
    id.long.var = "Subject",
    point.args = rlang::list2(alpha = 0.3)
  ) +
  stat_summary(
    aes(group = 1),
    fun = "mean",
    geom = "line",
    linewidth = 1
  ) +
  stat_summary(
    geom = "errorbar",
    fun.data = "mean_sdl",
    fun.args = list(mult = 1),
    size = 1.1, 
    width = 0.06
    ) + 
  stat_summary(
    geom = "point",
    fun = "mean", 
    size = 3
    )
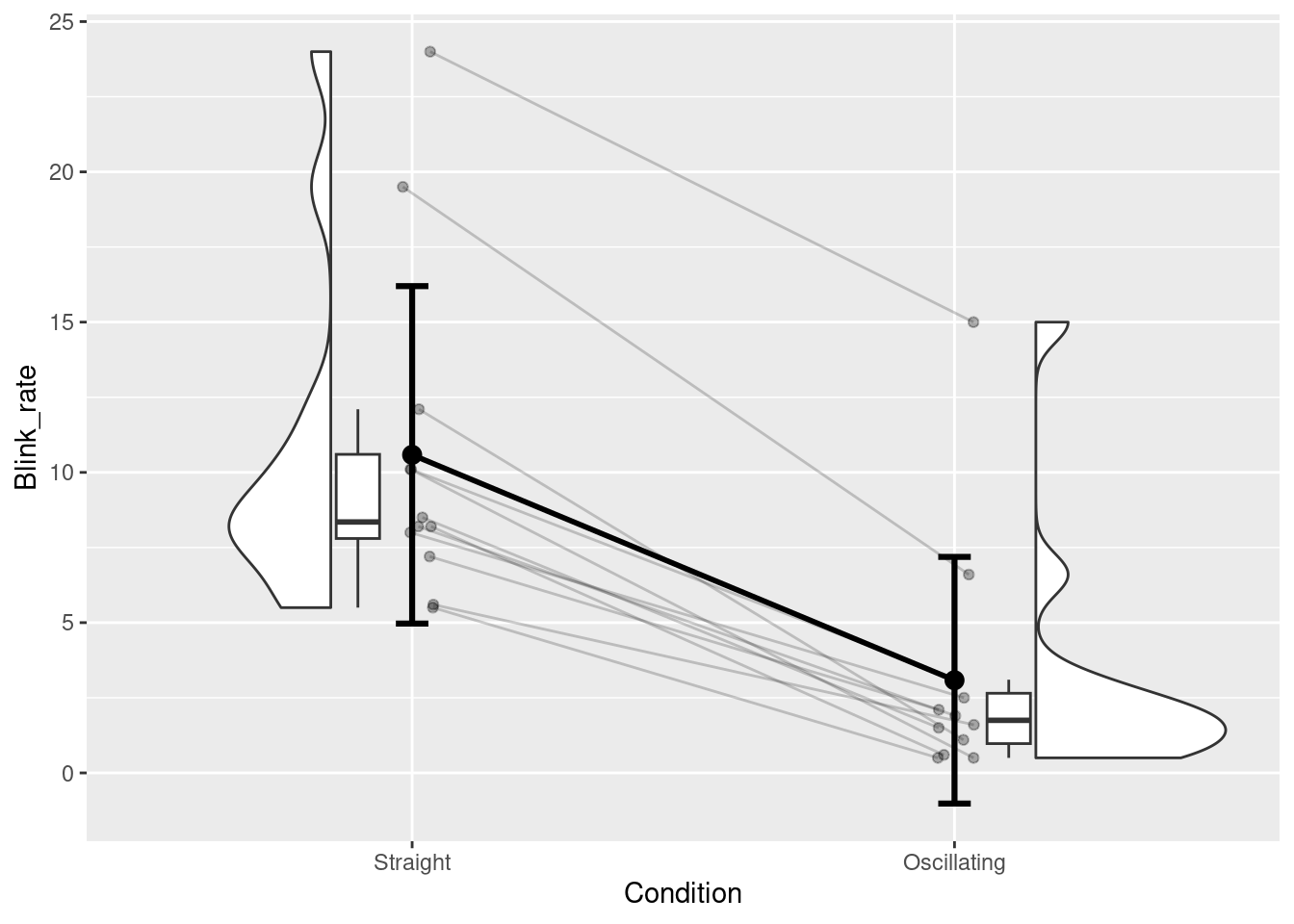
Exemple de graphique pour une comparaison de deux groupes de valeurs appariés (dépendants)

Figure 4.19: Exemple de graphique pour une comparaison de deux groupes de valeurs appariés (dépendants)

Le graphiques montré ci-dessus pour données appariées contient des éléments graphiques supplémentaires par rapport à celui proposé pour les données non appariées : des lignes reliant les données individuelles, et une ligne reliant les statistiques qui représentent les tendances centrales (ici les moyennes). Ces deux types d’éléments graphiques sont importants pour explicitement montrer qu’il y a un lien entre les deux conditions de mesure (il s’agit des mêmes individus et donc du même groupe), et cela permet de mettre en évidence à la fois les trajectoires individuelles et celle du groupe entre les deux conditions de mesure.

Pour obtenir ces éléments supplémentaires, il a fallu configurer l’argument id.long.var de la fonction geom_rain() pour indiquer le nom de la variable sur laquelle se baser pour garder l’appariement des données individuelles entre les deux conditions et ainsi permettre un bon tracé des lignes individuelles. La ligne reliant les moyennes a été ajoutée grâce à la fonctionstat_summary() avec la particularité d’indiquer 1 pour l’argument group de la fonction aes() associée à la fonction stat_summary(). Enfin, l’argument rain.side de la fonction geom_rain() a été configuré de telle sorte à avoir les données des deux groupes en vis-à-vis, mais un autre choix aurait pu être fait.

4.3.1.2 Étudier numériquement la relation

De manière générale, étudier la relation entre une variable quantitative et une variable qualitative revient souvent à comparer les valeurs que prend la variable quantitative en fonction des modalités de la variable qualitative. L’observation de différences de scores entre les modalités pourrait alors indiquer qu’il y a un lien entre la variable qualitative (qu’on pourrait appeler variable facteur) et la variable quantitative (qu’on pourrait appeler variable réponse). À noter que la démonstration d’un lien de cause à effet entre la variable quantitative et la variable qualitative ne pourra être effective que si l’on a sciemment fait varier les modalités de la variable qualitative pour en observer la conséquence sur les valeurs de la variable quantitative.

De prime abord, l’analyse qui pourrait être envisagée pour comparer deux groupes serait d’utiliser simplement la différence entre les moyennes des deux groupes. Toutefois, en se restreignant à cela, il pourrait être difficile de porter un jugement sur la grandeur relative de la différence entre les groupes comparés, qu’on pourrait appeler taille d’effet. Il serait également difficile de comparer cette taille d’effet avec celles observées dans d’autres études, en particulier celles traitant de thématiques différentes, car en étant calculée de la sorte, la taille d’effet serait inhérente à la nature des variables investiguées et à la grandeur des valeurs mesurées dans l’étude. Il est donc intéressant, dans ce genre de situations, de standardiser la différence de scores obtenue entre les deux groupes. Dans la littérature, la procédure de standardisation a été très développée pour la comparaison de moyennes. Pour cette raison, les sous-parties suivantes qui traitent de la comparaison de deux groupes présentent essentiellement les calculs pour obtenir une taille d’effet en vue de comparer des moyennes. Ces calculs sont repris de l’article de Lakens (2013). Quelques mots seront toutefois donnés pour les situations pour lesquelles ces calculs risqueraient de ne pas être appropriés.

4.3.1.2.1 Cas de deux groupes de données indépendants (données non appariées)

\(d_{s}\) et \(d_{av}\) de Cohen

Classiquement, l’indice statistique utilisé pour calculer une différence de moyennes de manière standardisée entre deux groupes de données non appariées, à partir d’échantillons de population, est le \(d_{s}\) de Cohen. Cette statistique se calcule en faisant la différence entre les moyennes des deux groupes à comparer, et en divisant cette différence par l’écart-type combiné (ou commun) des deux groupes. Ce calcul est montré ci-dessous :

\[d_{s} = \frac{\overline{X}_{1} - \overline{X}_{2}} {\sqrt{\frac{(N_{1} - 1) \hat{\sigma}_{1}^2 + (N_{2} - 1) \hat{\sigma}_{2}^2} {N_{1} + N_{2} - 2}}},\]

avec \(\overline{X}_{1}\) et \(\overline{X}_{2}\) les moyennes des deux groupes comparés, \(N_{1}\) et \(N_{2 }\) les effectifs respectifs des deux groupes comparés, et \(\hat{\sigma}_{1}^2\) et \(\hat{\sigma}_{2}^2\) les variances respectives des deux groupes comparés. On peut remarquer qu’au dénominateur, la variance d’un groupe donné est multipliée par un coefficient calculé à partir de l’effectif du groupe, cela pour que le poids de la variance d’un groupe dans le calcul final soit ajusté par rapport à la taille du groupe représenté. Dans R, si l’on voulait calculer \(d_s\) manuellement, cela donnerait ceci (à partir du jeu de données iris_two_species) :

# Calcul des paramètres
X1 <- iris_two_species %>% filter(Species == "setosa") %>% pull(Sepal.Length) %>% mean()
X2 <- iris_two_species %>% filter(Species == "versicolor") %>% pull(Sepal.Length) %>% mean()
SD1 <- iris_two_species %>% filter(Species == "setosa") %>% pull(Sepal.Length) %>% sd()
SD2 <- iris_two_species %>% filter(Species == "versicolor") %>% pull(Sepal.Length) %>% sd()
N1 <- iris_two_species %>% filter(Species == "setosa") %>% pull(Sepal.Length) %>% length()
N2 <- iris_two_species %>% filter(Species == "versicolor") %>% pull(Sepal.Length) %>% length()

# Calcul de ds
ds <- (X1 - X2) / sqrt(((N1-1) * SD1^2 + (N2-1) * SD2^2) / (N1+N2-2))
ds
## [1] -2.104197

Heureusement, le \(d_{s}\) de Cohen peut être facilement calculé à l’aide de la fonction cohens_d() du package effectsize, qui nécessite d’être installé puis chargé avant d’être utilisé :

library(effectsize)
cohens_d(
  Sepal.Length ~ Species, 
  data = iris_two_species, 
  paired = FALSE, 
  pooled_sd = TRUE
  )
## Cohen's d |         95% CI
## --------------------------
## -2.10     | [-2.59, -1.61]
## 
## - Estimated using pooled SD.

Dans cet exemple, on remarque qu’on a bien cherché à savoir comment les données de la variable Sepal.Length pouvaient différer en fonction (~) des modalités de la variable Species. Si la fonction nous donne un résultat, il faut toutefois bien faire attention au sens du calcul qui a été réalisé. Configurée de la sorte, la fonction cohens_d() réalise la différence modalité 1 - modalité 2. Il faut donc savoir quelle est la modalité 1 et quelle est la modalité 2 dans la variable Species pour ensuite pouvoir interpréter le signe du résultat, qui est négatif ici avec la valeur de -2.10. Pour ce faire, on peut utiliser la fonction levels() :

levels(iris_two_species$Species)
## [1] "setosa"     "versicolor" "virginica"

L’ordre des modalités affichées nous indique que setosa est la modalité 1, et que versicolor est la modalité 2. (On remarque par ailleurs que le jeu de données iris_two_species contient toujours trois modalités à la suite du filtrage précédent du jeu de données iris à l’aide de la fonction filter()). Par conséquent, le \(d_{s}\) de Cohen de -2.10 obtenu plus haut indique que la longueur des sépales (Sepal.Length) pour l’espèce setosa est inférieure à celles des sépales de l’espèce versicolor. Cette interprétation est en cohérence avec le graphique réalisé au préalable (cf. Figure 4.18). Si l’on avait voulu avoir le calcul inverse (versicolor - setosa), il aurait fallu reconfigurer l’ordre des modalités, par exemple à l’aide de la fonction fct_relevel() du package forcats comme montré à la fin du chapitre 3.

De manière importante, le calcul de \(d_s\) à partir d’un échantillon en vue d’avoir une estimation dans la population suppose que les variances des deux groupes dans la population d’intérêt soient similaires. Si cette supposition n’est pas valide ou est non désirée, alors il peut être préconisé de calculer un autre indicateur appelé \(d_{av}\) (cf. https://aaroncaldwell.us/TOSTERpkg/articles/SMD_calcs.html), lequel consiste à diviser la différence de moyennes par un écart-type moyen :

\[d_{av} = \frac{\overline{X}_{1} - \overline{X}_{2}} {\sqrt{\frac{\hat{\sigma}_{1}^2 + \hat{\sigma}_{2}^2} {2}}}\]

En repartant des paramètres calculés précédemment, on peut manuellement obtenir cet indice comme ceci :

# Calcul de dav
dav <- (X1 - X2) / sqrt((SD1^2 + SD2^2) / 2)
dav
## [1] -2.104197

On peut obtenir le \(d_{av}\) avec le package effectsize comme ceci (avec pooled = FALSE) :

cohens_d(
  Sepal.Length ~ Species, 
  data = iris_two_species, 
  paired = FALSE, 
  pooled_sd = FALSE
  )
## Cohen's d |         95% CI
## --------------------------
## -2.10     | [-2.60, -1.60]
## 
## - Estimated using un-pooled SD.

On note que les valeurs de \(d_s\) et de \(d_{av}\) ne changent pas dans nos exemples car chaque modalité de la variable Species est associée au même nombre d’individus, ce qui revient à faire des calculs similaires pour les deux indices statistiques obtenus jusqu’à présent.

Malheureusement, il se trouve que \(d\) (\(d_s\) ou \(d_{av}\)) est indicateur qui est biaisé positivement lorsqu’il s’agit d’estimer la différence de moyennes standardisée à l’échelle de la population d’intérêt. Par « biaisé positivement », il faut comprendre que si une multitude d’études s’intéressait à calculer \(d\) et qu’on faisait la moyenne des résultats trouvés, alors on aurait une surestimation de la magnitude de la valeur de \(d\) dans la population (il s’agit d’un fait qui peut être démontré avec des simulations sur un ordinateur), cela notamment dans le cas ou les études utiliseraient de petits échantillons (N < 20), selon Hedges et Okins (1985) cités par Lakens (2013).

\(g_{s}\) et \(g_{av}\) de Hedges

Pour régler le problème de biais que pose le \(d\) de Cohen, un autre indicateur statistique a été proposé : le \(g\) de Hedges. Il s’agit en réalité du \(d\) de Cohen, mais qu’on modifie grâce à l’utilisation d’un facteur de correction. Une approximation de \(g\) est montrée ci-dessous (2013) :

\[g = d (1 - \frac{3}{4(N_{1} + N_{2}) - 9}),\]

avec \(d\) le \(d_s\) ou le \(d_{av}\) de Cohen, et \(N_{1}\) et \(N_{2}\) les effectifs respectifs des deux groupes comparés. En réalité, le calcul exact du facteur de correction est relativement complexe, et est montré avec l’équation ci-dessous (Kelley, 2005) :

\[g = d \frac{\Gamma(\frac{df}{2})}{\sqrt{\frac{df}{2}\Gamma(\frac{df-1}{2})}} \]

avec \(\Gamma\) la loi Gamma, et \(df\) ce qu’on appelle le nombre de degrés de liberté (qui est ici égal au nombre total d’individus moins 2). Dans les faits, les différences entre \(d\) et \(g\) sont minimes, surtout avec \(N\) > 20 dans les groupes.

Dans R, le \(g_{s}\) de Hedges lié à un échantillon de population peut être calculé à l’aide de la fonction hedges_g() du package effectsize :

hedges_g(
  Sepal.Length ~ Species,
  data = iris_two_species, 
  paired = FALSE, 
  pooled_sd = TRUE
  )
## Hedges' g |         95% CI
## --------------------------
## -2.09     | [-2.57, -1.60]
## 
## - Estimated using pooled SD.

Ici, la valeur ne change pas beaucoup par rapport à \(d_s\) car l’effectif n’est pas si petit que cela (\(N_{1}\) + \(N_{2}\) = 100 ici, ce qui fait que la correction appliquée au \(d_{s}\) de Cohen est minime).

Le \(g_{av}\) de Hedges lié à un échantillon de population peut aussi être calculé à l’aide de la fonction hedges_g() du package effectsize (avec pooled = FALSE) :

hedges_g(
  Sepal.Length ~ Species,
  data = iris_two_species, 
  paired = FALSE, 
  pooled_sd = FALSE
  )
## Hedges' g |         95% CI
## --------------------------
## -2.09     | [-2.58, -1.58]
## 
## - Estimated using un-pooled SD.

Par principe, il pourrait être recommandé de toujours utiliser le \(g\) (\(g_s\) ou \(g_{av}\)) de Hedges (Lakens, 2013).

Qualification de l’importance de la différence de moyennes standardisée

Une fois que l’on a calculé une taille d’effet, il est toujours intéressant d’essayer de formuler un jugement sur l’importance, l’ampleur de l’effet. En ce sens, des valeurs seuils ont été proposées dans la littérature (Cohen, 1988; in Lakens (2013)). Ces valeurs, valables pour interpréter des tailles d’effet dans le cadre d’une étude de type between-subject design, sont montrées dans le tableau ci-dessous.

``` ```{=html}
(\#tab:effectsizetable)Termes pour qualifier la taille d'effet dans le cadre d'une comparaison de moyennes associées à des variables indépendantes

Petit

Moyen

Grand

>=0.2

>=0.5

>=0.8

La classification montrée dans ce tableau doit être utilisée avec précaution car en réalité, l’importance d’un effet s’apprécie aussi au regard du contexte dans lequel il s’applique. Les valeurs du tableau donnent donc des repères généraux mais ne peuvent pas au final servir d’étalon universel (Lakens, 2013).

Il existe également une autre approche pour interpréter une valeur de taille d’effet : l’approche Common Language explanation (Lakens, 2013). Cette approche consiste à faire le lien entre la valeur de la taille d’effet et les probabilités de rencontrer des valeurs similaires ou supérieures dans un groupe en comparaison à un autre. Par exemple, lorsqu’on obtient un \(d_{s}\) de Cohen de 0.80, cela peut se traduire par le fait qu’il y a 71.4 % de chances qu’une personne prise au hasard dans le groupe avec la meilleure moyenne ait un score plus élevé qu’une personne qui serait prise au hasard dans le groupe avec la moyenne la plus basse des deux groupes. Kristoffer Magnusson a réalisé une page web qui permet d’utiliser l’approche Common Language explanation pour n’importe quelle valeur de taille d’effet dans le cadre d’une étude de type between-subject design. Jetez donc un oeil au lien suivant pour plus de détails : https://rpsychologist.com/cohend.

Delta de Glass

Dans certains cas où l’on souhaiterait comparer les scores de deux groupes indépendants pour tester l’effet de deux conditions expérimentales différentes, l’expérimentation en tant que telle peut influencer, au-delà de la moyenne, l’écart-type de la variable réponse dans un des deux groupes. On peut se trouver dans ce genre de situation lorsque l’on compare les données post-programme d’un groupe entraîné ou traité à celles d’un groupe contrôle. En effet, le groupe entraîné/traité peut voir son écart-type changé au terme d’un programme en raison d’une réponse individuelle hétérogène à ce programme, ce qui ne sera pas en principe le cas du groupe contrôle. Dans ce genre de situations, des indices statistiques autres que le \(d\) de Cohen ou le \(g\) de Hedges mériteraient d’être calculés, tels que le delta (\(\Delta\)) de Glass (Lakens, 2013) :

\[\Delta = \frac{\overline{X}_{1} - \overline{X}_{2}} {\hat{\sigma}_{2}}\]

Le calcul du \(\Delta\) de Glass est dans l’idée le même que celui du \(d\) de Cohen, sauf que la différence entre les moyennes des deux groupes n’est pas divisée par un écart-type lié aux deux groupes, mais par l’écart-type d’un seul des deux groupes, qui serait en principe celui qui représenterait la condition contrôle ou la condition de référence. Une pratique souvent recommandée pour comparer dans ce genre de situation les scores post-programme de deux groupes (un groupe entraîné/traité et un groupe contrôle) serait d’utiliser l’écart-type des scores du groupe contrôle obtenu en pré-programme (Lakens, 2013).

Dans R, le \(\Delta\) de Glass lié à un échantillon de population peut être calculé à l’aide de la fonction glass_delta() du package effectsize. Attention, l’écart-type utilisé dans le code suivant est celui de la variable quantitative associée à la modalité 2 de la variable qualitative, qui est toujours versicolor dans cet exemple (exemple dont le contexte n’est certes pas celui d’un programme dont on cherche l’effet, mais le principe d’utilisation du code reste le même).

glass_delta(Sepal.Length ~ Species, 
            data = iris_two_species)
## Glass' delta (adj.) |         95% CI
## ------------------------------------
## -1.77               | [-2.25, -1.29]

Notons quand même que l’utilisation du \(\Delta\) de Glass semble peu courante dans les études cherchant à tester l’effet d’un programme. L’une des difficultés liées à son utilisation est que cela suggère que les groupes à comparer soient identiques en pré-programme pour la variable étudiée. En général, des procédures un peu plus sophistiquées sont utilisées pour déterminer l’effet d’un programme, en particulier des procédures qui permettent de prendre en compte justement les différences qui peuvent exister entre les groupes en pré-programme.

Cas particuliers

Certaines situations peuvent rendre la comparaison de moyennes non pertinente. C’est par exemple le cas lorsque l’un des deux groupes (voire les deux) présentent des données aberrantes ou très extrêmes, en particulier en présence de petits échantillons. L’utilisation des moyennes dans ce cas pourrait ne pas être pertinente car ces moyennes ne refléteraient alors pas correctement les tendances centrales (et donc les groupes associés). Dans ces cas là, mieux vaut observer les médianes de chaque groupe et chercher à voir si les distributions sont en décalage ou non.

4.3.1.2.2 Cas de deux groupes de données dépendants (données appariées)

\(d_{z}\) et \(d_{av}\) de Cohen

Le calcul classique pour obtenir la taille d’effet désignant l’écart de moyennes entre deux groupes de données dépendants est celui du \(d_{z}\) (Lakens, 2013), qui est montré ci-dessous :

\[d_{z} = \frac{\overline{X} _{diff}}{\hat{\sigma}_{diff}},\]

\(\overline{X}_{diff}\) désignant la moyenne des différences relatives à chaque pair de valeurs obtenues dans les deux conditions comparées, et \(\hat{\sigma}_{diff}\) désignant l’écart-type de ces différences.

Dans R, on peut calculer manuellement \(d_z\) comme ceci (avec le jeu de données Blink) :

# Calcul des paramètres
diff <- Blink$Straight - Blink$Oscillating
mean_diff <- mean(diff)
sd_diff <- sd(diff)

# Calcul de dz
dz <- mean_diff / sd_diff
dz
## [1] 2.811462

Le \(d_{z}\) peut heureusement être obtenu à nouveau avec la fonction cohens_d() du package effectsize. Pour illustrer cela, nous allons utiliser le jeu de données Blink2 crée plus haut pour l’exemple de graphique :

cohens_d(
  Pair(Blink_rate[Condition == "Straight"], Blink_rate[Condition == "Oscillating"]) ~ 1, 
  data = Blink2
  )
## Cohen's d |       95% CI
## ------------------------
## 2.81      | [1.51, 4.09]

Parce que la valeur de \(d_z\) dépend de la corrélation entre les deux groupes de valeurs comparés, certains auteurs préfèrent rapporter un autre indice statistique qui n’a pas cette propriété et qui en ce sens pourrait être davantage comparable au \(d\) de Cohen obtenu dans les études avec groupes indépendants. Parmi les candidats possibles, il y a notamment le \(d_{av}\) de Cohen (Lakens, 2013), dont la formule est montrée ci-dessous :

\[d_{av} = \frac{\overline{X} _{diff}}{\sqrt{\frac{\hat{\sigma}_{1}^2 + \hat{\sigma}_{2}^2} {2}}}\]

Ce calcul reviendrait donc à diviser la moyenne des différences (qui est égale à la différence de moyennes) par l’écart-type moyen relatif aux deux groupes de données. Manuellement cela donnerait (avec Blink2) :

# Calcul des paramètres
X1 <- Blink2 %>% filter(Condition == "Straight") %>% pull(Blink_rate) %>% mean()
X2 <- Blink2 %>% filter(Condition == "Oscillating") %>% pull(Blink_rate) %>% mean()
SD1 <- Blink2 %>% filter(Condition == "Straight") %>% pull(Blink_rate) %>% sd()
SD2 <- Blink2 %>% filter(Condition == "Oscillating") %>% pull(Blink_rate) %>% sd()
N1 <- Blink2 %>% filter(Condition == "Straight") %>% pull(Blink_rate) %>% length()
N2 <- Blink2 %>% filter(Condition == "Oscillating") %>% pull(Blink_rate) %>% length()

# Calcul de dav
dav <- (X1 - X2) / sqrt((SD1^2 + SD2^2) / 2)
dav
## [1] 1.525146

Pour obtenir \(d_{av}\) avec des données appariées et la fonction cohens_d(), il faut procéder comme s’il s’agissait de données non appariées :

cohens_d(
  Blink_rate ~ Condition,
  data = Blink2,
  paired = FALSE, 
  pooled_sd = FALSE
  )
## Cohen's d |       95% CI
## ------------------------
## 1.53      | [0.58, 2.44]
## 
## - Estimated using un-pooled SD.

\(g_{z}\) et \(g_{av}\) de Hedges

Comme pour les \(d\) de Cohen calculés dans le cadre de groupes indépendants, les \(d\) de Cohen obtenus avec groupes dépendants sont positivement biaisés. À nouveau, ces indices statistiques peuvent être corrigés avec le même facteur de correction montré pour le \(g\) de Hedges dans la partie sur les groupes dépendants. Toutefois, \(g_{av}\) ne serait malgré tout pas complètement non biaisé (Lakens, 2013).

Pour obtenir \(g_z\) :

hedges_g(
  Pair(Blink_rate[Condition == "Straight"], Blink_rate[Condition == "Oscillating"]) ~ 1, 
  data = Blink2
  )
## Hedges' g |       95% CI
## ------------------------
## 2.61      | [1.41, 3.80]

Pour obtenir \(g_{av}\) :

hedges_g(
  Blink_rate ~ Condition,
  data = Blink2, 
  paired = FALSE, 
  pooled_sd = FALSE
  )
## Hedges' g |       95% CI
## ------------------------
## 1.47      | [0.56, 2.35]
## 
## - Estimated using un-pooled SD.

Cas particuliers

Lorsque la présence de valeurs aberrantes peut fausser le calcul de la taille d’effet que l’on cherche à caractériser dans la population étudiée, une première idée pourrait être ici de faire la différence des médianes des deux groupes. Toutefois, comme le rappellent Weissegerber et al. (2015), cette approche n’est mathématiquement pas correcte pour caractériser l’évolution typique des scores étudiés. La bonne méthode est de calculer la médiane des différences. Le code ci-dessous présente donc le calcul de la médiane des différences, ici à partir du jeu de données Blink. La visualisation graphique correspondante pourrait être alors un raincloud plot pour une seule variable, celle des différences entre les deux conditions. Le code pour ce type de graphiques a été vu au chapitre précédent.

# Calcul de la médiane des différences
 Blink %>%
  mutate(Difference = Straight - Oscillating) %>%
  summarise(median_diff = median(Difference))
##   median_diff
## 1           7

4.3.2 Comparaison de trois groupes de données et plus

…