Chapitre 3 Analyses univariées

Réaliser une analyse descriptive univariée signifie que l’on s’intéresse à une seule variable en particulier. L’enjeu est ici de prendre connaissance de la distribution de la variable, c’est-à-dire de la manière selon laquelle se répartissent les observations en fonction des valeurs que prend la variable. De manière complémentaire, l’analyse descriptive univariée vise à prendre connaissance des indices statistiques qui caractérisent la variable, ainsi qu’à déterminer ceux qui seraient les plus pertinents pour la résumer.

Dans cette partie, les notions de population et d’échantillon vont revenir à plusieurs reprises. La notion de population désigne tous les individus existant qui satisfont à un ou plusieurs critères particuliers (e.g., les adultes de moins de 30 ans). En général, lorsque l’on souhaite étudier un phénomène dans une population cible, il est impossible de prendre en compte tous les individus de la population en question. L’alternative est alors de conduire l’étude sur un échantillon, c’est-à-dire une fraction de la population composée d’individus qui représentent la population étudiée. La distinction entre population et échantillon est importante à faire à plusieurs égards. Si une étude n’a pu être conduite que sur un échantillon, cela implique de mettre en oeuvre des procédures statistiques pour estimer avec plus ou moins d’incertitude le résultat réel concernant la population étudiée, cela à partir du résultat trouvé dans l’échantillon observé. La seule analyse descriptive de l’échantillon ne suffit donc pas en soi à décrire une population. En revanche, lorsque l’étude a pu être conduite sur l’ensemble de la population à étudier (e.g., l’équipe de France dans un sport donné), il n’y a par définition pas lieu de chercher à conduire des procédures statistiques particulières pour estimer le résultat réel pour la population en question. Dans ce chapitre, les procédures d’analyse proposées servent en général à seulement décrire la variable telle qu’elle est donnée à voir à partir des données que l’on a en sa possession. L’objectif n’est donc pas ici de discuter particulièrement des statistiques les plus pertinentes à utiliser lorsqu’il s’agit de chercher à résumer la distribution d’une variable à l’échelle d’une population à partir d’un échantillon initial. Pour le moment, il s’agit d’être en mesure de décrire l’échantillon (ou la population si les données obtenues concernent toute la population) que l’on a sous les yeux.

Dans le cadre de cette partie, nous allons commencer à voir comment produire des graphiques dans RStudio, et par là-même, découvrir progressivement le package ggplot2. Le package ggplot2 n’est pas le plus simple à utiliser lorsque l’on découvre le logiciel R. D’ailleurs, de nombreux manuels portant sur R privilégient les packages et fonctions de base de R lorsqu’il s’agit de montrer comment obtenir des graphiques relativement simples pour analyser ses données. Cependant, les packages et fonctions de base de R sont rapidement limités lorsqu’il s’agit de réaliser des graphiques relativement complexes. Le parti pris ici est donc d’initier dès à présent à l’utilisation du package ggplot2 pour réaliser des graphiques, même simples, afin de pouvoir être plus rapidement à l’aise dès lors qu’il s’agira par la suite de produire des graphiques relativement élaborés à l’aide de ce package. Cependant, l’ambition n’est pas ici de permettre la maîtrise complète du package ggplot2. Pour cela, il vaut mieux se référer à des documentations spécialisées telles que la seconde édition de l’ouvrage ggplot2 d’Hadley Wickham (2016), en sachant qu’une troisième édition est en cours de développement et est accessible en ligne ici : https://ggplot2-book.org.

3.1 Variables quantitatives

3.1.1 Visualiser la distribution de la variable

Dans le cadre de l’analyse de variables quantitatives, il est toujours utile de d’abord visualiser graphiquement la distribution des données à l’aide d’un histogramme. Un histogramme, c’est un graphique avec des barres dont la largeur représente un intervalle donné de valeurs numériques, et dont la hauteur représente le nombre d’observations associées à une valeur qui est située dans l’intervalle en question. Plus une barre est haute, plus il y a d’observations concernées par l’intervalle de valeurs. Un exemple d’histogramme est montré sur la Figure 3.1.

ggplot(data = iris, aes(x = Sepal.Length)) + 
  geom_histogram(fill = "white", color = "black")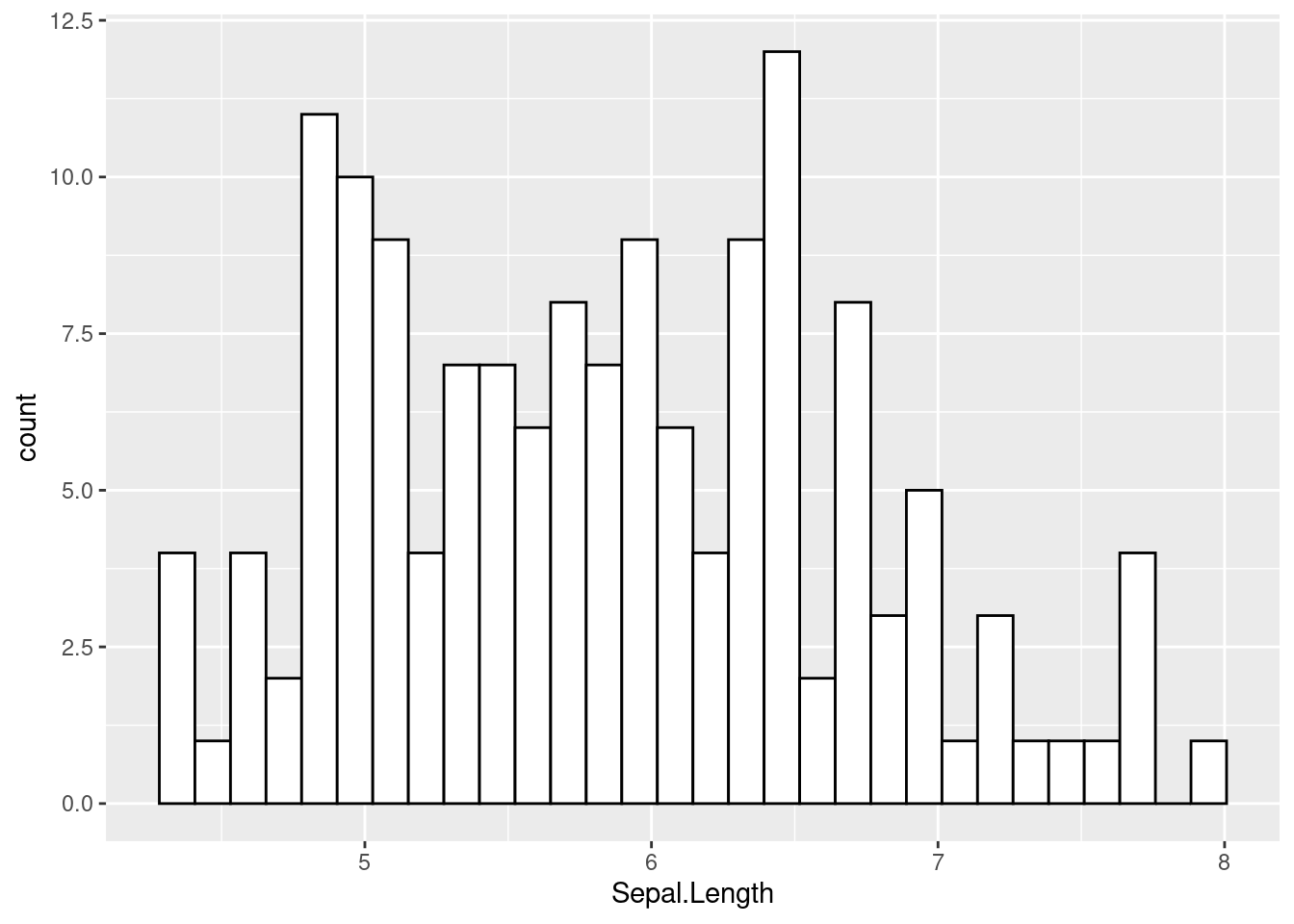

Figure 3.1: Exemple d’histogramme

Pour générer cet histogramme, nous avons utilisé les fonctions ggplot() et geom_histogram() du package ggplot2. La fonction ggplot() est nécessaire pour initier le graphique. Si on lance la commande ggplot() dans la Console, on peut voir qu’un écran grisé apparaît à droite de l’écran du PC dans la fenêtre Plots de RStudio. Cet écran grisé est tel un tableau vierge qui ne demande qu’à être complété grâce à des commandes supplémentaires que l’on doit préciser dans le code. Dans le code montré ci-dessus, on remarque que la fonction ggplot() a été configurée à l’aide de deux éléments : l’argument data, et la fonction aes(). L’argument data permet de désigner le jeu de données à partir duquel n’importe quelle autre fonctionnalité du package ggplot2 sera utilisée si rien d’autre n’est précisé dans le reste du code. Comme on peut le voir, le jeu de données utilisé ici est iris, que nous avons déjà rencontré dans la partie précédente. La fonction aes(), elle, permet de désigner les données à partir desquelles les éléments graphiques indiqués par la suite devront être réalisés. Dans le cadre d’une analyse univariée, nous n’avons besoin que d’une seule variable. Celle-ci peut être renseignée à droite de x =, et on aura reconnu dans le code ci-dessus le nom d’une variable effectivement présente dans le jeu de données iris. Une fois que ces informations sont renseignées, nous ne sommes pas encore en mesure de voir un quelconque graphique. Pour cela, il faut que la fonction ggplot() soit accompagnée d’une fonction qui permette d’indiquer quel type de graphique on veut. C’est à cela que sert ici la fonction geom_histogram(). On peut noter que l’ajout de cette fonction a été réalisé grâce au signe +, en écrivant la fonction après ce signe. La fonction geom_histogram() aurait pu être écrite directement après le symbole +, mais pour des raisons de lisibilité, nous sommes allés à la ligne. (Attention : Aller à la ligne avant le signe + n’est en revanche pas possible.) De manière intéressante et importante pour la suite, on pourra noter que dans ce cas de figure, nous aurions pu aussi utiliser le symbole pipe (|>) pour enchaîner la création d’un graphique à la suite de l’écriture du jeu de données comme cela :

iris |>
  ggplot(aes(x = Sepal.Length)) +
  geom_histogram(fill = "white", color = "black")

# On remarque ici que l'argument `data = ` dans `ggplot()` a dû être enlevé.

Comme l’indique le message qui accompagne le graphique, l’histogramme a été réalisé sur la base de 30 bins. Cela signifie que pour faire ce graphique, R a découpé en 30 intervalles égaux l’intervalle allant de la valeur la plus faible de la variable (i.e., le minimum) à la valeur la plus élevée de la variable (i.e., le maximum). Il s’agit de la méthode par défaut utilisée par la fonction geom_histogram(). Toutefois, cette méthode par défaut n’est pas vraiment adaptée, comme cela l’est indiqué d’ailleurs dans la documentation d’aide associée à cette fonction. Et puis, lorsqu’il s’agit d’appréhender au mieux la distribution d’une variable avec un histogramme, une bonne pratique est d’observer ce qu’il se passe avec différentes largeurs de bins. La largeur d’une bin peut être modifiée à l’aide de l’argument binwidth. L’unité de la valeur associée à cet argument correspond à l’unité de la variable étudiée (cf. code ci-dessous et Figure 3.2).

# Graphique avec binwidth = 0.3
ggplot(data = iris, aes(x = Sepal.Length)) +
  geom_histogram(binwidth  = 0.3,
                 fill = "white",
                 color = "black") +
  ggtitle("binwidth = 0.3")

# Graphique avec binwidth = 0.7
ggplot(data = iris, aes(x = Sepal.Length)) +
  geom_histogram(binwidth  = 0.7,
                 fill = "white",
                 color = "black") +
  ggtitle("binwidth = 0.7")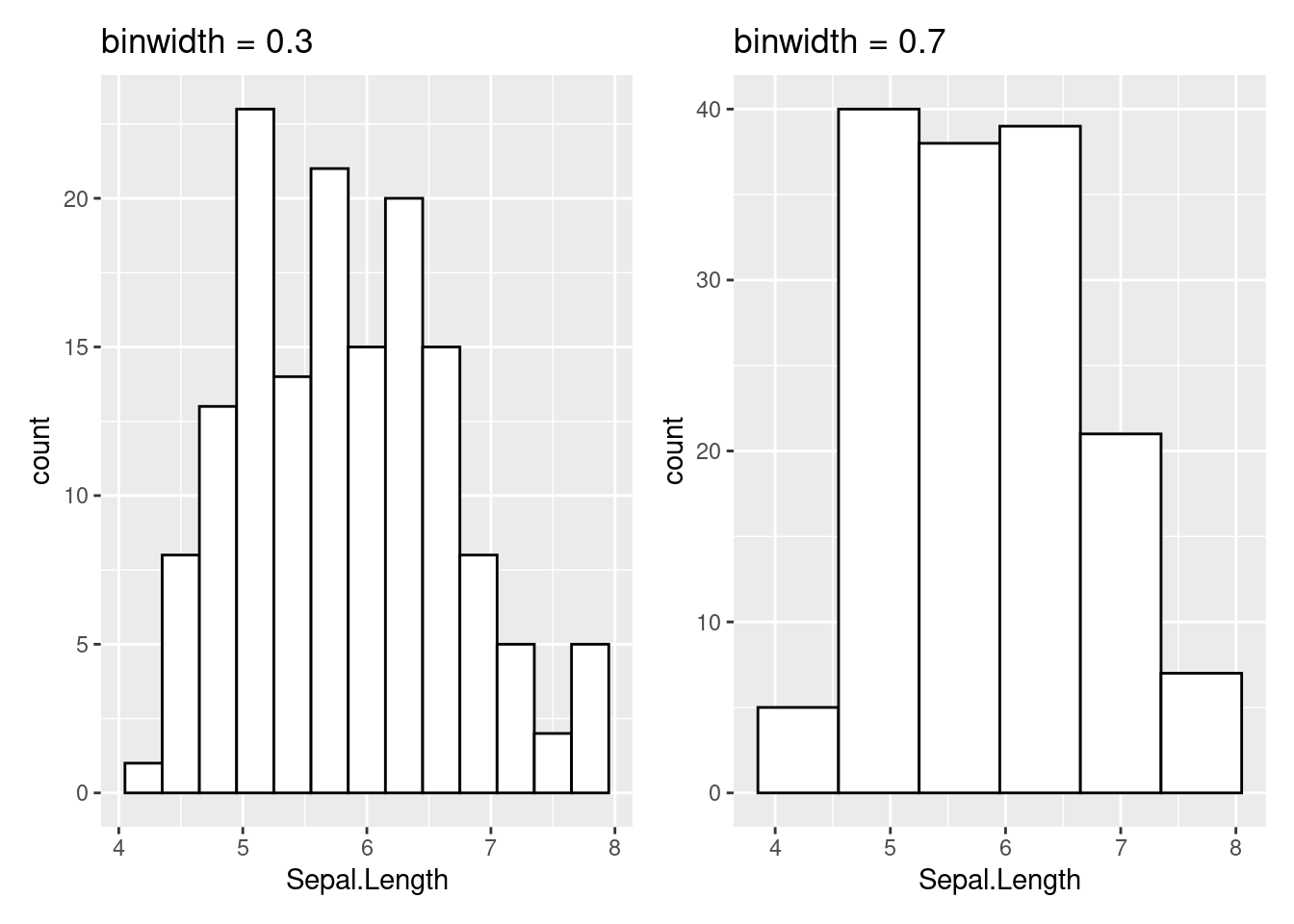

Figure 3.2: Différentes largeurs d’intervalles pour un histogramme

En plus de l’histogramme, une autre manière de prendre connaissance graphiquement de la distribution des données d’une variable quantitative est d’utiliser une boîte à moustaches. Pour ce faire, il convient d’utiliser la fonction geom_boxplot(), comme montré dans le code ci-dessous. Le résultat de ce code est montré sur la Figure 3.3. On pourra noter ci-dessous l’ajout d’une ligne de code avec une fonction theme() dont on ne présentera pas les détails ici ; cette fonction nous sert juste ici à ne pas montrer des chiffres qui auraient été ajoutés par défaut sur l’axe Y de gauche du graphique et qui n’auraient eu aucun intérêt.

ggplot(data = iris, aes(x = Sepal.Length)) +
  geom_boxplot() +
  theme(axis.text.y = element_blank(),
        axis.ticks.y = element_blank())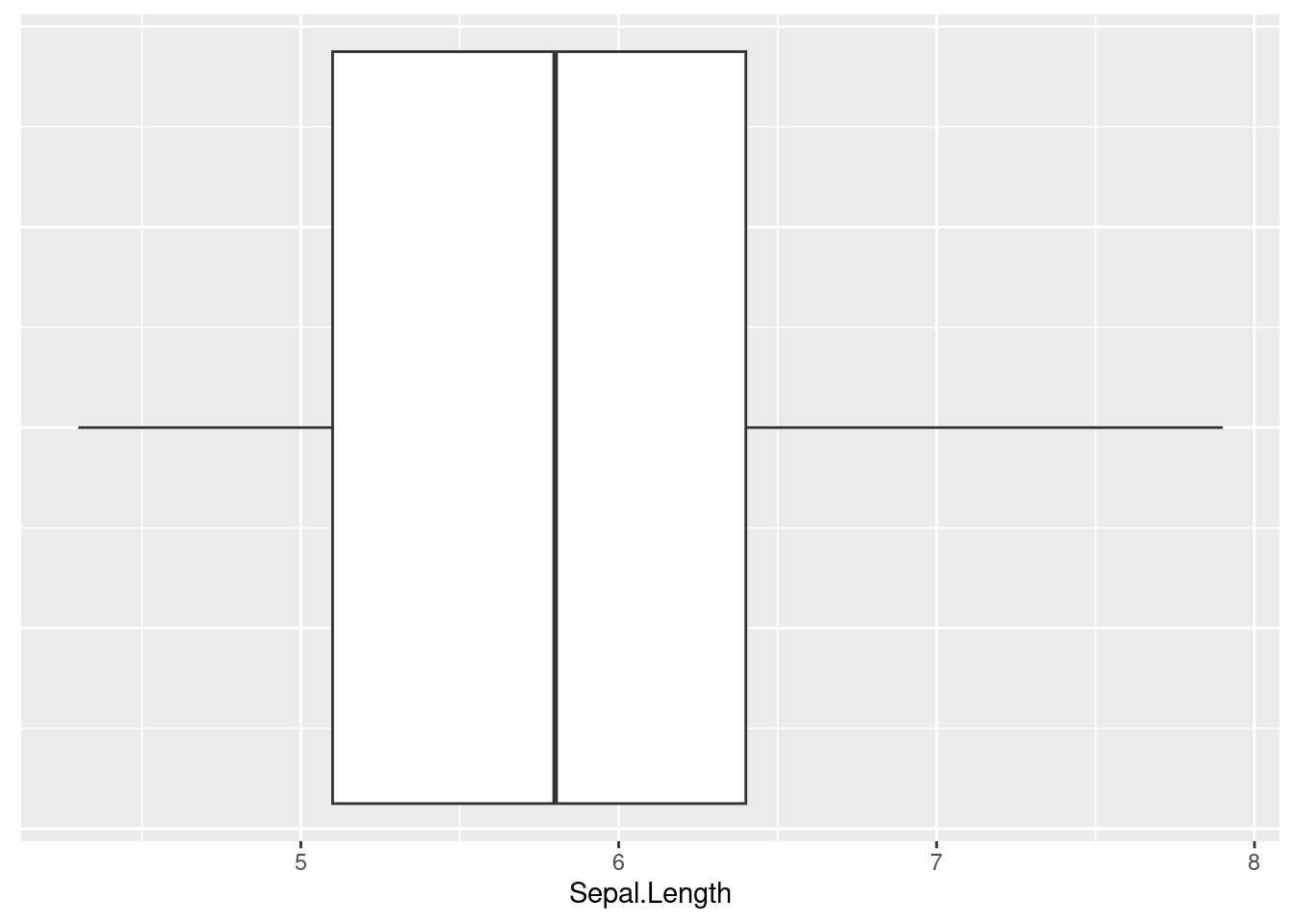

Figure 3.3: Exemple de boîte à moustaches

La boîte à moustaches (cf. Figure 3.3) nous livre plusieurs informations. Tout d’abord, ses extrémités nous indiquent ce qu’on appelle le premier quartile (ici représenté par le bord gauche de la boîte) et le troisième quartile (ici représenté par le bord droit de la boîte). Le premier quartile (Q1) désigne la valeur en-dessous de laquelle on retrouve 25 % des observations de la variable (i.e., 25 % des observations sont associées à une valeur plus faible que Q1), alors que le troisième quartile (Q3) représente la valeur en-dessous de laquelle on retrouve 75 % des observations (i.e., 75 % des observations sont associées à une valeur plus faible que Q3). Cela indique alors que sur la Figure 3.3, l’intervalle qui sépare le bord gauche du bord droit de la boîte contient 50 % des observations. La ligne noire à l’intérieur de la boîte blanche désigne la médiane, qui est la valeur pour laquelle on a 50 % des observations qui ont une valeur inférieure à cette valeur repère, et pour laquelle on a 50 % des observations qui ont une valeur supérieure à cette valeur repère. Les lignes noires en-dehors de la boîte sont les moustaches. Dans le cas présent, la moustache de gauche s’étend jusqu’à la valeur minimale de la variable, et la moustache de droite s’étend jusqu’à la valeur maximale de la variable. Si le minimum (ou le maximum) avait été éloigné de la boîte de plus de 1.5 fois la différence entre Q3 et Q1 (qu’on appelle l’intervalle interquartile), l’extrémité de la moustache se serait arrêtée à la dernière valeur avant cette limite, et toute valeur ayant dépassé cette limite aurait été représentée par un point. Pour illustrer ce dernier cas de figure, on peut modifier manuellement une valeur de la variable Sepal.Length du jeu de données iris de telle sorte à ce qu’il y ait une nouvelle valeur qui soit particulièrement éloignée de la boîte. Une telle valeur s’appelle un outlier (cf. Figure 3.4).

# On modifie ici, pour l'exemple, la valeur de la 3ème observation
# en lui assignant la valeur 12.
iris$Sepal.Length[3] <- 12

# Obtention du graphique
ggplot(data = iris, aes(x = Sepal.Length)) +
  geom_boxplot() +
  theme(axis.text.y = element_blank(),
        axis.ticks.y = element_blank())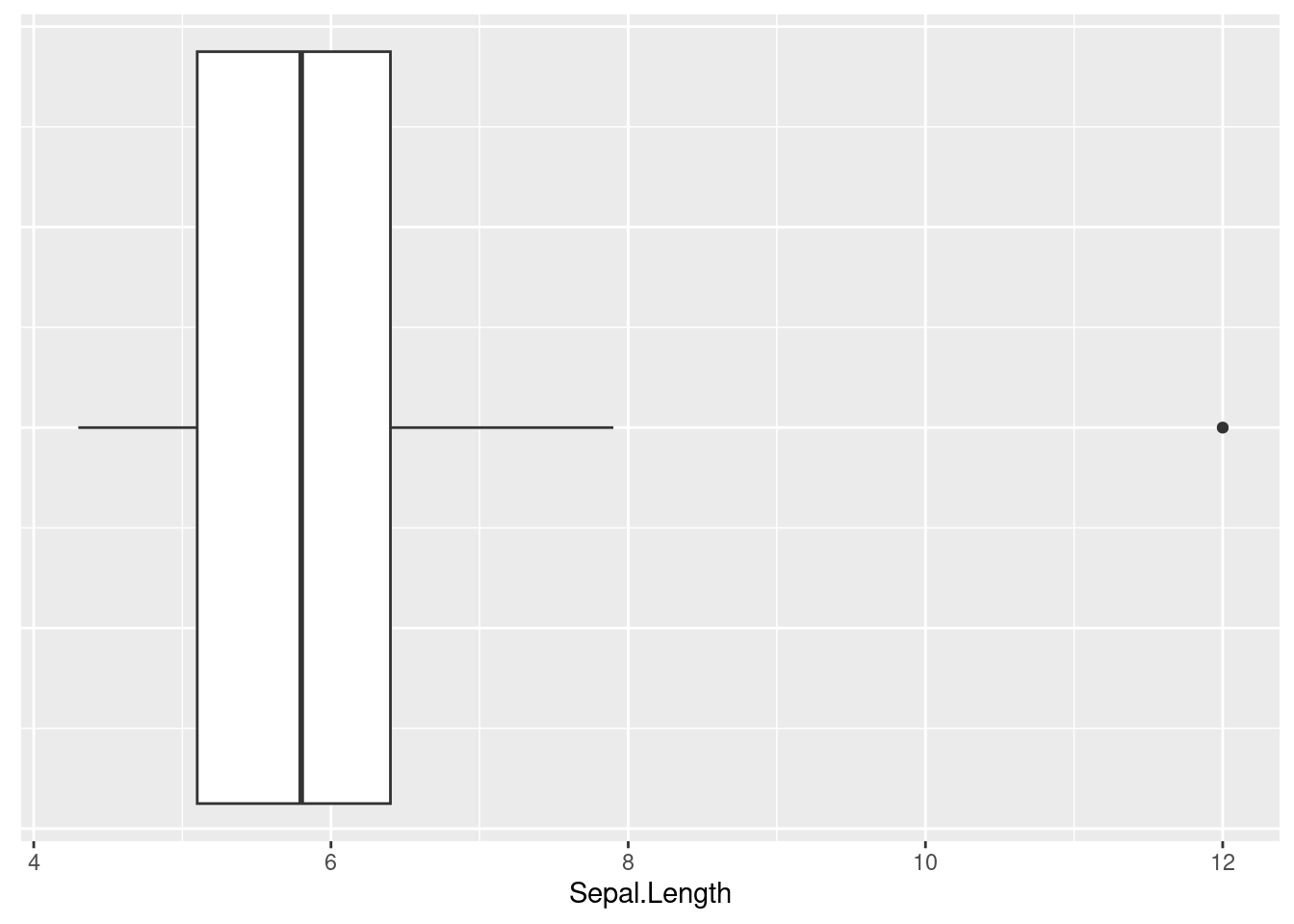

Figure 3.4: Visualisation d’un outlier

Une boîte à moustaches a donc notamment l’intérêt de mettre en évidence des valeurs qui apparaissent comme “étranges” par rapport au reste des données. Lorsqu’il semble évident que l’outlier est une valeur erronée, ou quand on veut tout simplement vérifier qu’il s’agit d’une erreur ou non, il est intéressant de savoir à quelle observation (i.e., à quel individu dans certains contextes) cette valeur étrange appartient, pour ensuite éventuellement la corriger. Malheureusement, la fonction geom_boxplot() ne dispose pas d’argument pour permettre d’identifier facilement à quelle observation appartient cette valeur. Cependant, on peut s’appuyer sur des fonctions créées manuellement dans R pour parvenir à cela. Dans ce cas de figure, le site https://stackoverflow.com est souvent intéressant car riche de solutions. C’est d’ailleurs en provenance de ce site que vient la fonction montrée ci-dessous (voir ici) qui va nous permettre ensuite de savoir, à partir du graphique, à quelle observation correspond cette donnée étrange.

is_outlier <- function(x) {
  x < quantile(x, 0.25) - 1.5 * IQR(x) |
    x > quantile(x, 0.75) + 1.5 * IQR(x)
}

Voici donc, ci-dessus, à quoi ressemble une fonction à son état brut, avec : le nom de la fonction à gauche de la flèche d’assignation (<-), la commande function() qui permet d’amorcer la création de la fonction, et les lignes de code entre les accolades { } qui indiquent les actions que la fonction réalise. La seule chose qu’il faut comprendre à ce stade, c’est que cette fonction, qui va donc s’appeler par la suite is_outlier(), a besoin pour fonctionner qu’on lui indique un nom de variable (représenté par la lettre x dans le code ci-dessus), et que le résultat de cette fonction sera une nouvelle variable qui contiendra seulement des TRUE ou des FALSE, en sachant que TRUE correspondra au fait que la valeur de la variable étudiée était un outlier, et que FALSE correspondra au fait que la valeur de la variable étudiée n’était pas un outlier. (Notons ici que la définition d’un outlier est la même que celle décrite plus haut, à savoir une valeur qui serait éloignée de Q1 ou de Q3 de plus de 1.5 fois l’intervalle interquartile.) Mais regardons concrètement ce que donne cette fonction lorsqu’elle est appliquée à la variable Sepal.Length du jeu de données iris (NB : La fonction ne marchera que si elle a été activée/créée auparavant) :

is_outlier(x = iris$Sepal.Length)

##   [1] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [11] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [21] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [31] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [41] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [51] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [61] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [71] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [81] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [91] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [101] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [111] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [121] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [131] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [141] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

Quand on regarde bien, on voit que la troisième observation de cette nouvelle variable que l’on vient de créer (seulement de manière temporaire ici car on ne l’a pas assignée à un nom) contient la valeur TRUE, ce qui est en accord avec la valeur que nous avons introduite auparavant dans la variable Sepal.Length. Le fait d’observer ces valeurs TRUE et FALSE n’est évidemment pas une stratégie très pratique pour déterminer à quelle observation correspondrait l’outlier, et c’est pourquoi l’étape suivante consiste à montrer comment on peut se servir de cette fonction is_outlier() pour faire apparaître sur un graphique de boîte à moustaches les observations à qui appartiendraient les valeurs étranges (cf. Figure 3.5).

iris |>
  # Ajout d'un numéro id pour les observations
  mutate(id = as.factor(rep(1:50, times = 3)),
         # Création d'une nouvelle variable appelée id_outlier
         id_outlier = ifelse(is_outlier(x = Sepal.Length), id, "")) |>
  ggplot(aes(x = Sepal.Length, y = "")) +
  geom_boxplot() +
  # Ajout des numéros id des outliers
  geom_text(aes(label = id_outlier),  hjust = -1) +
  theme(
    axis.text.y = element_blank(),
    axis.ticks.y = element_blank(),
    axis.title.y = element_blank()
  )

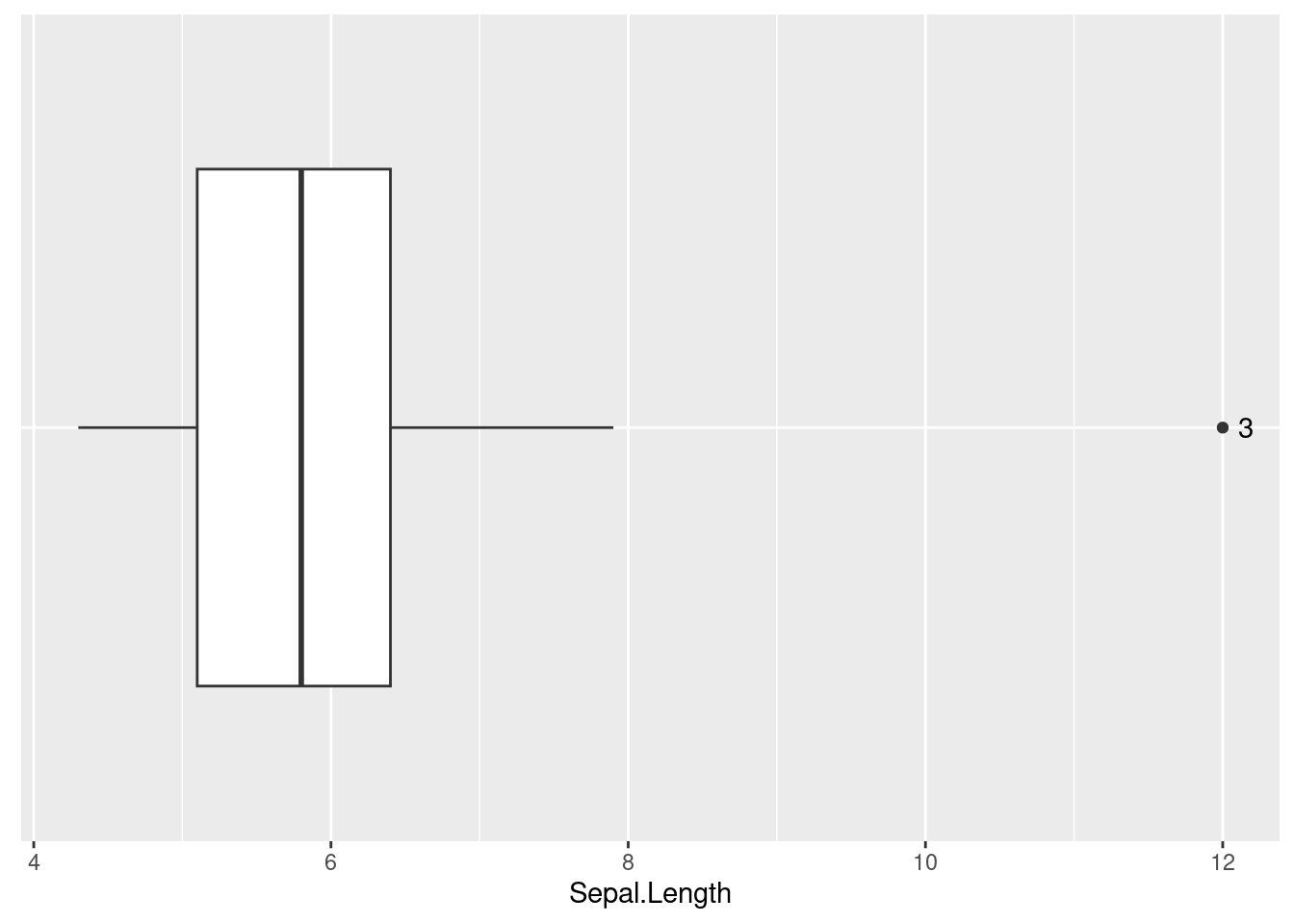
Figure 3.5: Identification d’un outlier

Il y a plusieurs choses à expliquer par rapport au graphique de la Figure 3.5 qui comporte à présent le numéro id associé à l’observation pour laquelle nous avions modifié la valeur. Tout d’abord, il faut noter qu’avant de créer le graphique, nous avons ajouté temporairement au jeu de données, avec la fonction mutate(), la variable id_outlier. Cette variable a été créée à l’aide de deux fonctions en réalité : la fonction ifelse(), et la fonction is_outlier() qu’on a présentée succinctement plus haut. Ici, la fonction ifelse() a fonctionné comme cela : si la fonction id_outlier() renvoyait la valeur TRUE, alors on conservait le numéro id de la variable Sepal.Length, sinon, on ne mettait rien. Cela veut dire que la variable id_outlier ne contenait que les numéros id pour lesquels la fonction is_outlier() avait renvoyé la valeur TRUE. Pour visualiser ce qu’il s’est passé, on peut revoir la conséquence du début du code qui a permis de faire le graphique (cf. colonne de droite dans le résultat ci-dessous) :

iris |>
  mutate(id = as.factor(rep(1:50, times = 3)),
         id_outlier = ifelse(is_outlier(x = Sepal.Length), id, "")) |>
  dplyr::select(id, Sepal.Length, id_outlier)

## # A tibble: 150 × 3
##    id    Sepal.Length id_outlier
##    <fct>        <dbl> <chr>     
##  1 1              5.1 ""        
##  2 2              4.9 ""        
##  3 3             12   "3"       
##  4 4              4.6 ""        
##  5 5              5   ""        
##  6 6              5.4 ""        
##  7 7              4.6 ""        
##  8 8              5   ""        
##  9 9              4.4 ""        
## 10 10             4.9 ""        
## # ℹ 140 more rows

Une fois cette procédure réalisée, le reste du code, et notamment la fonction geom_text(), a permis d’ajouter des éléments textuels au graphique, en l’occurrence en s’appuyant sur la variable id_outlier, tel que configuré avec la fonction aes() à l’intérieur de la fonction geom_text(). Lorsque la valeur anormale identifiée est effectivement une erreur de saisie dans la base de données, il convient de corriger la valeur avec la fonction d’assignation comme nous l’avons fait précédemment :

iris$Sepal.Length[3] <- 4.7  
# Le nombre entre crochets désigne la position de l'observation 
# dans la variable.

On remarque ainsi qu’au-delà de prendre connaissance de la forme de la distribution, passer par ces étapes graphiques permet aussi de s’assurer qu’il n’y a pas eu d’erreur lors de la saisie des données dans la base (du moins, pas d’erreur visible et qui risquerait d’impacter grandement les calculs futurs). Passer par l’analyse graphique est donc recommandé avant de pouvoir se fier aux résultats numériques que l’on pourrait calculer par la suite, tels que les indices statistiques qui permettent de résumer numériquement une variable.

À noter que si l’histogramme et la boîte à moustaches sont des graphiques classiques pour étudier la distribution d’une variable quantitative, il est aussi possible avec R de créer ce qu’on appelle un raincloud plot, tel qu’illustré sur la Figure 3.6. Un post du blog de Cédric Scherer fournit une description très intéressante et riche de l’intérêt de ce type de graphique. Le raincloud plot se compose de trois éléments (cf. figure ci-après) :

Une aire sous la courbe représentative de la densité de probabilité (the cloud), qui représente une estimation de la fréquence d’apparition d’une valeur donnée dans l’échantillon étudié. Cet élément est intéressant pour prendre pleinement conscience de la forme de la distribution. Attention cependant, car les formes des aires et les idées qu’elles donnent des distributions dans la population d’intérêt dépendent beaucoup du nombre d’observations disponibles, et leur utilisation pourrait donc se discuter en présence de peu d’observations.
Une boîte à moustaches, qui permet de se faire une idée résumée relativement robuste des distributions dans la population d’intérêt (i.e., insensible aux outliers et davantage comparable avec d’autres études) ; selon les cas, d’autres statistiques, comme les moyennes et les écarts-types, peuvent être utilisées à la place ou en plus des boîtes à moustaches (Allen et al., 2019).
Un nuage de points des données individuelles (the rain), qui est très intéressant pour avoir une vue précise des valeurs obtenues par les individus, de leurs différences éventuelles, des outliers éventuels, voire des patterns de distribution éventuellement inattendus ; les données individuelles permettent aussi d’avoir une idée plus claire de la grandeur du nombre d’observations présentes dans le jeu de données (chose non renseignée par les deux éléments précédents).

Parce qu’ils montrent les données individuelles, les raincloud plots vont dans le sens du propos de Weissgerber et al. (2015) qui militent pour la disparition des graphiques en forme de simples bâtons de dynamite, lesquels ayant été souvent utilisés par le passé pour montrer des moyennes et écart-types dans les études. Le problème de ces graphiques en forme de bâtons de dynamite est qu’ils peuvent induire en erreur quant à la réelle forme de la distribution et ils limitent les possibilités du lecteur de juger de la pertinence des choix d’analyses inférentielles qui seraient faits par la suite. Les raincloud plots peuvent être réalisés relativement facilement à l’aide de la fonction geom_rain() du package ggrain comme montré ci-dessous.

library(ggrain)

ggplot(data = iris, aes(1, Sepal.Length)) +
  geom_rain(
    fill = "grey",
    boxplot.args =  rlang::list2(fill = "white"),
    point.args = rlang::list2(alpha = 0.3, size = 3)
  ) +
  coord_flip(xlim = c(0.9, 1.5)) +
  theme(
    axis.text.y = element_blank(),
    axis.ticks.y = element_blank(),
    axis.title.y = element_blank()
  )

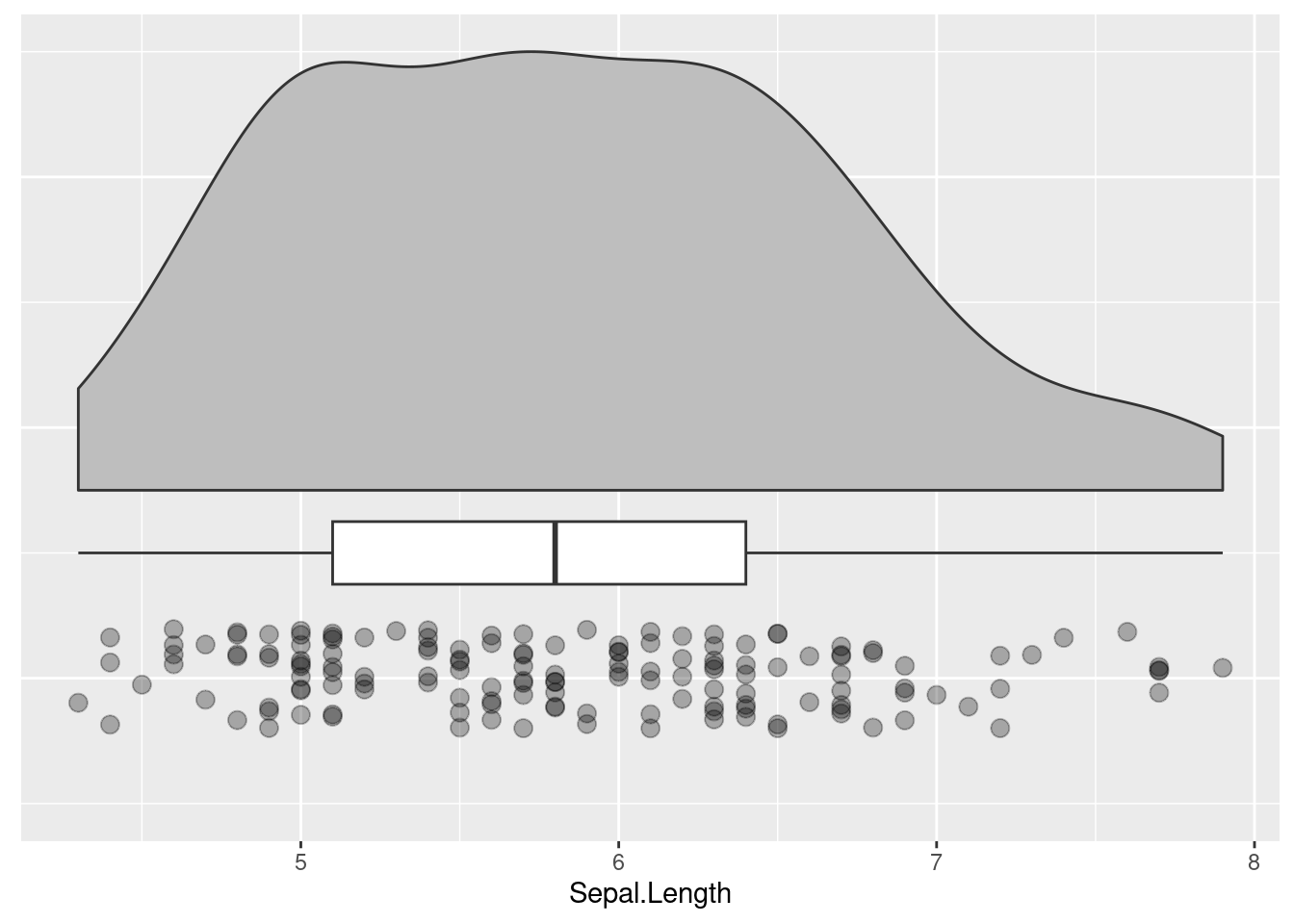
Figure 3.6: Exemple de raincloud plot

Lors de l’analyse de données, différentes formes typiques de distribution peuvent être rencontrées, notamment des formes gaussiennes, asymétriques, leptocurtiques, et platycurtiques (Dart & Chatellier, 2003). Ces formes sont illustrées sur la Figure 3.7. Les formes gaussiennes sont observées en présence de variables suivant ce qu’on appelle une loi normale. Très souvent, on associe une distribution gaussienne, et donc une loi normale, à une distribution en forme de cloche, bien que l’analogie à la cloche pourrait se discuter. Les formes asymétriques traduisent le fait que la majorité des observations sont concentrées sur une extrémité de l’intervalle des valeurs possibles, et qu’il existe des observations, non majoritaires, avec des valeurs pouvant être très éloignées de la majorité des données, mais seulement d’un seul côté de la distribution. Enfin, les formes leptocurtiques et platycurtiques sont appelées ainsi par comparaison à la forme gaussienne. En présence d’une forme leptocurtique, la distribution s’avère plus pointue, avec des queues (qui sont les extrémités de la distribution) plus longues qu’avec une forme gaussienne. Dans le cadre d’une distribution platycurtique, la distribution est plus aplatie, avec des queues plus courtes qu’avec une forme gaussienne (Dart & Chatellier, 2003). La distribution uniforme est un cas particulier de distribution platycurtique, et c’est cette distribution qui est en réalité montrée sur la Figure 3.7.

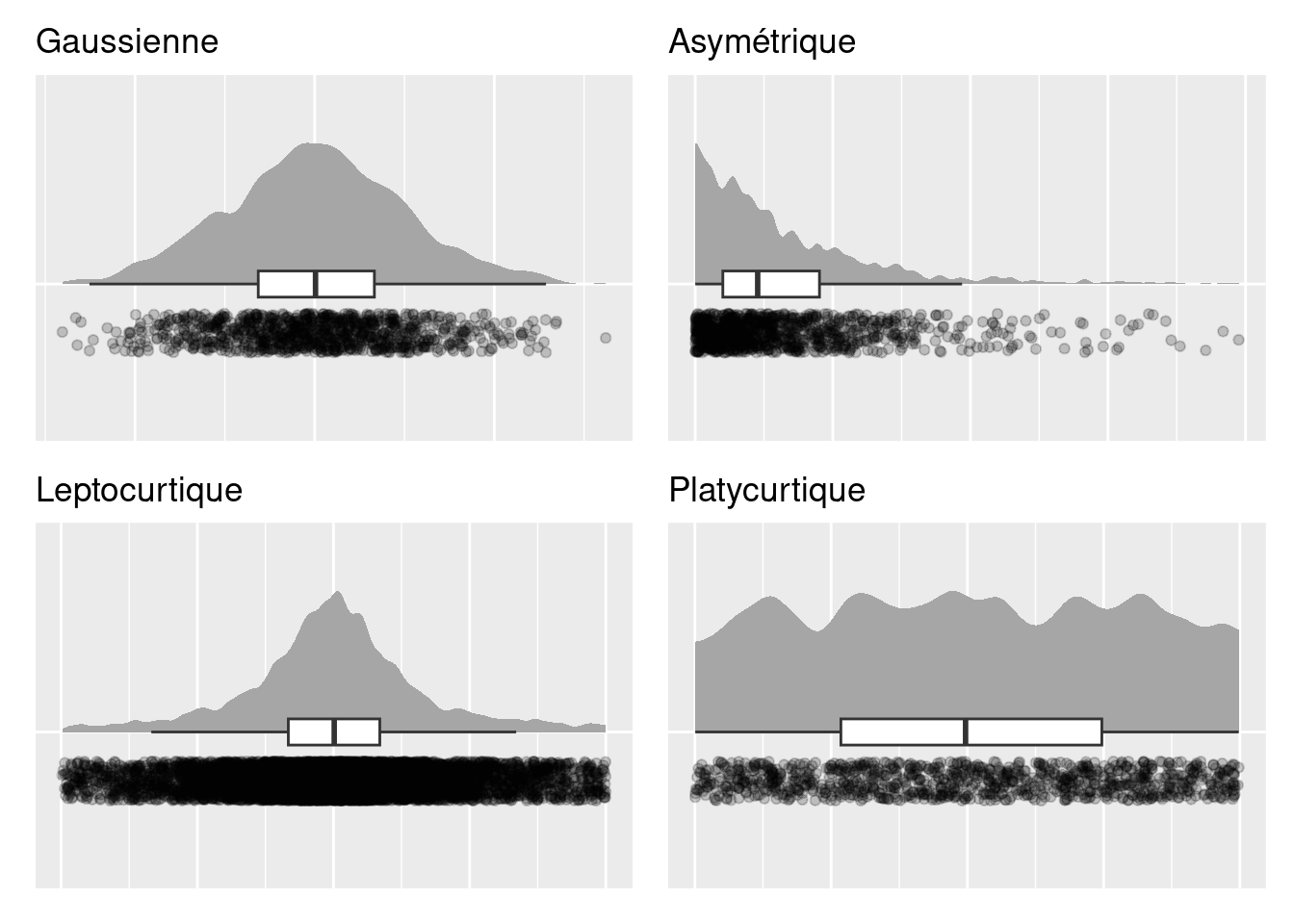
Figure 3.7: Différents types de distributions

La confiance que l’on peut avoir dans des résultats issus d’analyses inférentielles dépend de l’adéquation entre, d’une part, la forme de la distribution de la population d’où vient l’échantillon, et d’autre part, l’indice statistique choisi pour résumer la distribution de l’échantillon, en particulier sa position, pour conduire les analyses inférentielles. Il est donc important de chercher à savoir, graphiquement dans un premier temps, si la distribution de la variable est effectivement gaussienne ou non dans la population d’intérêt, cela à partir de l’échantillon que l’on a sous les yeux. Le fait d’être capable d’identifier les autres formes de distribution peut être aussi important afin de mener des analyses appropriées. Dans les exemples montrés ci-dessus, les distributions ont été créées à partir de 1000 valeurs générées de manière aléatoire de telle sorte à suivre des lois prédéfinies et ainsi illustrer différentes distributions possibles. C’est pour cette raison que les formes de distribution montrées sur la figure ci-dessus sont si nettes. Lorsque l’on travaille dans certains domaines ou contextes, tel qu’avec l’être humain, il peut être compliqué d’obtenir autant de données, et les formes de distribution seront alors plus dures à identifier.

Une fois qu’une première analyse graphique des données a été réalisée, il peut être utile de chercher à résumer de manière numérique la variable. Plusieurs types de statistiques peuvent être utilisés à cet effet : les indices de position, les indices de dispersion, les indices d’asymétrie, et les indices d’aplatissement.

3.1.2 Les indices de position

Les indices de position servent à donner un ordre de grandeur de la variable. Autrement dit, ces indices permettent de positionner la variable sur une échelle de valeurs numériques. De plus, ces statistiques peuvent être utilisées pour donner une idée de ce qu’on appelle la tendance centrale, c’est-à dire-la valeur typique d’une distribution qui donne une bonne indication de la localisation de la majorité des observations (Rousselet & Wilcox, 2020). Différentes statistiques peuvent être étudiées à cette fin : la moyenne, la médiane, la moyenne rognée, et le mode.

La moyenne

Si l’on pose que \(N\) est le nombre de valeurs dans une variable (on parle également de taille de la variable), que \(i\) est la \(i\)-ème observation (\(i\)-ème position) dans la variable, et que \(X{i}\) est la valeur associée à la \(i\)-ème position, alors le calcul de la moyenne, notée \(\overline{X}\), peut être écrit de la manière suivante : \[\overline{X} = \frac{1}{N}\sum_{i=1}^{N} X{i}\] Cette expression mathématique signifie que la moyenne s’obtient en additionnant (\(\sum\)) les valeurs allant de la position 1 à la position \(N\) de la variable, et en divisant le tout par le nombre total de valeurs \(N\) contenues dans la variable. Pour mieux comprendre, prenons par exemple une variable qui ne contiendrait que les cinq premières valeurs de la variable Sepal.Length du jeu de données iris et qu’on appelle sample_iris.

sample_iris <- iris$Sepal.Length[1:5]
sample_iris

## [1] 5.1 4.9 4.7 4.6 5.0

La moyenne de la variable sample_iris peut alors s’obtenir en divisant la somme des valeurs de la variable par le nombre de valeurs contenues dans la variable, qui est ici de 5 :

(5.1 + 4.9 + 4.7 + 4.6 + 5.0) / 5

## [1] 4.86

Évidémment, ce n’est pas très pratique de fonctionner comme cela. Aussi, R permet de calculer directement la moyenne avec la fonction mean() :

mean(x = sample_iris)

## [1] 4.86

Dans certains cas, il se peut qu’il y ait des valeurs manquantes dans la variable à étudier. Ces valeurs manquantes sont en principe notées NA. Introduisons une valeur manquante dans notre variable sample_iris, et essayons de calculer la moyenne à nouveau :

sample_iris[2] <- NA
sample_iris

## [1] 5.1  NA 4.7 4.6 5.0

mean(x = sample_iris)

## [1] NA

Comme nous pouvons le voir ci-dessus, quand il y a une valeur manquante dans la variable, l’utilisation de la fonction mean() configurée par défaut renvoie la valeur NA, ce qui signifie que R n’a pas pu calculer de valeur moyenne, ce qui est normal car nous lui avons demandé de le faire en utilisant une valeur inconnue. Dans ce cas là, pour pouvoir faire le calcul de la moyenne seulement à partir des valeurs connues, il faut configurer la fonction pour que les valeurs manquantes ne soient pas considérées pour le calcul. L’argument à configurer dans ce cas là est na.rm en lui associant la valeur TRUE.

mean(x = sample_iris, na.rm = TRUE)

## [1] 4.85

La gestion des valeurs manquantes telle que nous venons de la voir s’effectue de la même manière avec beaucoup de fonctions dans R. Ainsi, il s’agira de fonctionner de la même manière avec la plupart des fonctions de base que nous pourrons rencontrer par la suite et qui seront concernées par ce genre de problème. Par ailleurs, si les exemples ci-dessus ont été réalisés à l’aide d’une variable isolée (i.e., ne faisant pas partie d’un tableau de données), c’est évidemment possible d’utiliser la fonction mean() directement à partir d’un tableau de données :

mean(x = iris$Sepal.Length)

## [1] 5.843333

La moyenne, c’est en quelque sorte le “centre de gravité” de la variable (Navarro, 2018). L’un de ses intérêts est que son calcul prend en compte toutes les informations contenues dans la variable, ce qui est utile quand on a relativement peu de données (Navarro, 2018). En revanche, un inconvénient est qu’elle est très sensible aux valeurs extrêmes, et en particulier aux valeurs qui seraient particulièrement basses ou particulièrement élevées par rapport à la majorité des valeurs de la variable (il s’agirait ici d’outliers), et cela est d’autant plus vrai lorsque la taille de l’échantillon étudié est faible. Dans ce dernier cas, il y a donc un risque assez important que la moyenne ne représente pas bien la tendance centrale, c’est-à-dire la valeur ou la zone de valeurs où sont situées la majorité des observations. Ce risque existe aussi même avec des tailles d’échantillon relativement importantes lorsque la distribution est asymétrique, comme illustré sur la Figure 3.8. Sur cette figure, on peut voir qu’avec une distribution gaussienne, la moyenne correspond parfaitement à la tendance centrale. En revanche, avec une distribution asymétrique à droite, on voit que la moyenne est “tirée vers la droite” par rapport à la tendance centrale sous l’effet des valeurs, certes moins nombreuses, mais d’une grandeur plus importante.

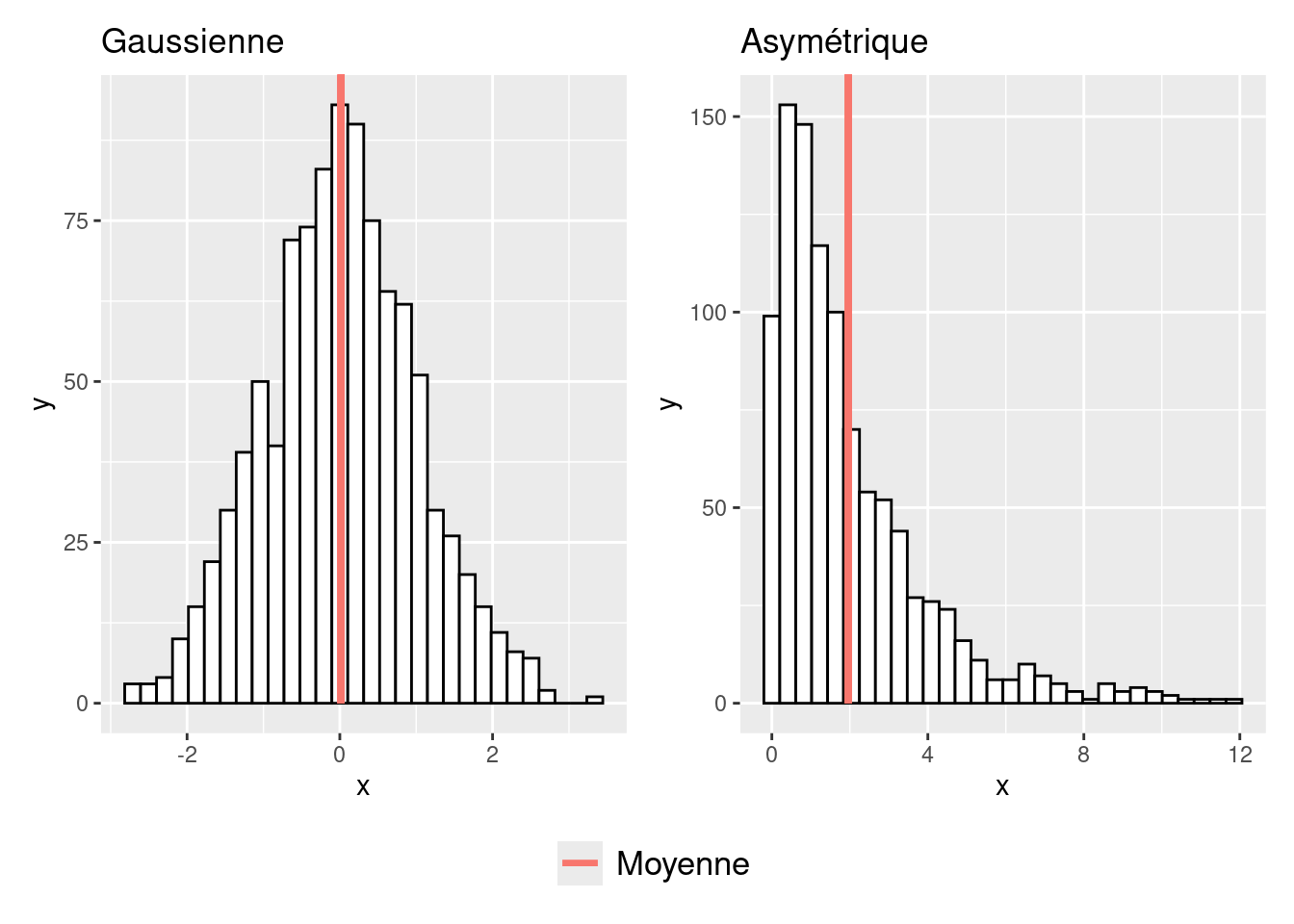
Figure 3.8: Effet de la forme de la distribution sur la position de la moyenne

La médiane

La médiane est le deuxième indice de position que l’on considère régulièrement lorsqu’il s’agit de résumer numériquement une variable quantitative. Pour l’obtenir, il faut d’abord classer les valeurs de la variable selon un ordre croissant. La médiane pour une variable de taille \(N\) est alors la valeur correspondant au rang (\(N\) + 1) / 2. Ainsi, la médiane désigne la valeur qui sépare les valeurs de la variable en deux groupes d’observations de même taille (Chatellier & Durieux, 2003). Dans l’exemple ci-dessous, il y a cinq observations, et donc cinq valeurs, qui ont été triées par ordre croissant. La médiane est alors la valeur correspondant au rang (5 + 1) / 2 = 3, soit 4.9.

##   1   2   3   4   5 
## 4.6 4.7 4.9 5.0 5.1

Dans le cas où le nombre d’observations contenues dans la variable étudiée serait un nombre pair, la médiane s’obtiendrait différemment. En effet, avec une variable qui contiendrait par exemple six valeurs, la médiane serait associée, selon la méthode expliquée ci-dessus, au rang (6 + 1) / 2 = 3.5, or ce rang n’existe pas. Dans ce cas, la médiane s’obtient en faisant la moyenne des deux nombres du milieu. Par exemple, ci-dessous, la médiane correspond à la moyenne des valeurs de la 3ème et de la 4ème observation, ce qui donne 4.95.

##   1   2   3   4   5   6 
## 4.6 4.7 4.9 5.0 5.1 5.4

Dans R, la médiane d’une variable s’obtient facilement à l’aide de la fonction median().

vec <- c(4.6, 4.7, 4.9, 5.0, 5.1, 5.4)
median(x = vec)

## [1] 4.95

Contrairement à la moyenne, la médiane prend donc en compte moins d’informations relatives aux données. Toutefois, en tant que valeur “du milieu”, la médiane présente l’intérêt de ne pas être influencée par les valeurs extrêmes. En raison de cela, la médiane est susceptible de mieux refléter la tendance centrale que la moyenne en présence de petits échantillons avec des outliers, ou en présence d’une forme de distribution asymétrique. Ce dernier cas est illustré sur la Figure 3.9.

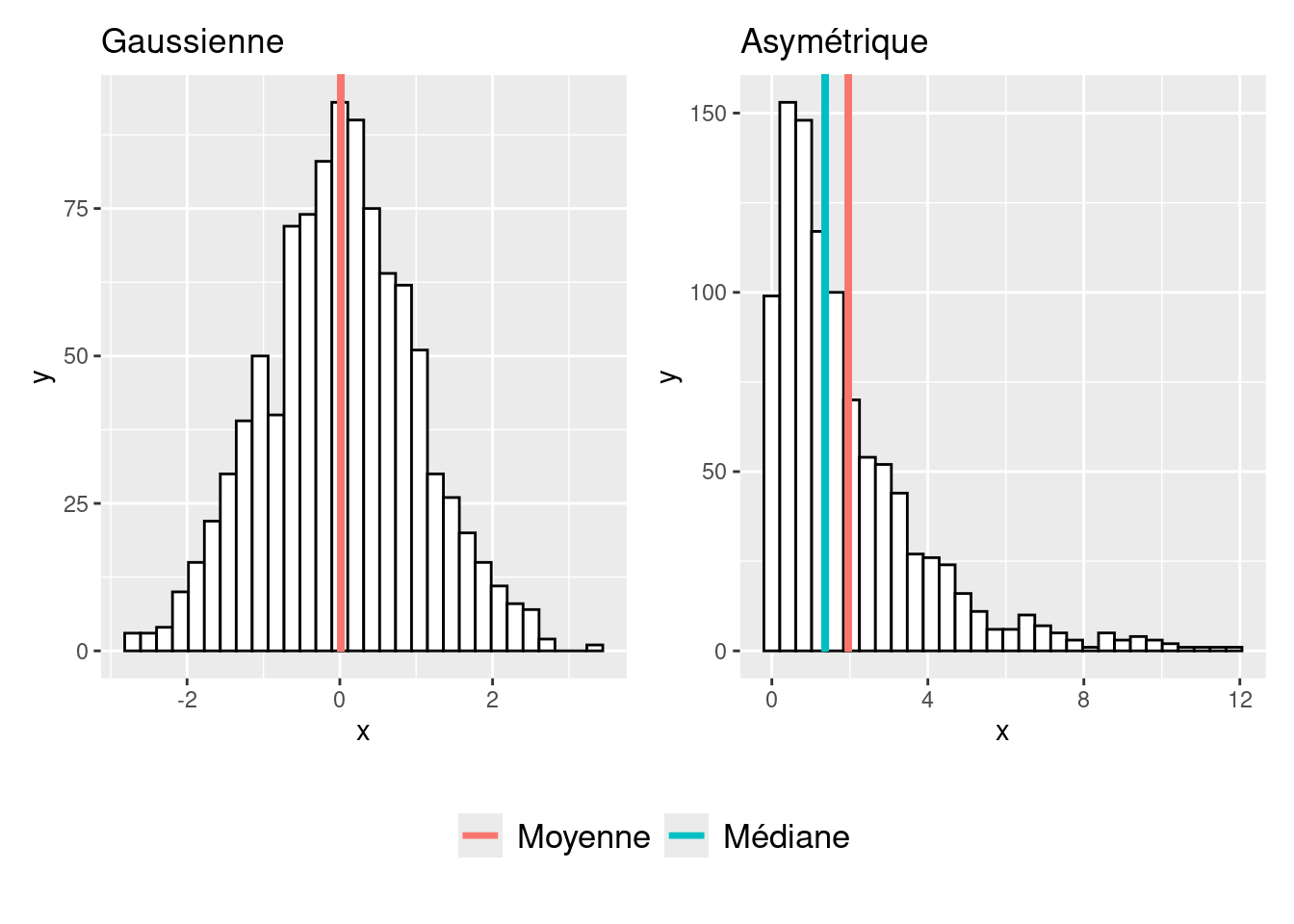
Figure 3.9: Effet de la forme de la distribution sur la position de la médiane

La moyenne rognée

Parfois, il est possible de rencontrer ce qu’on appelle la moyenne rognée. Le principe est ici de calculer la moyenne non pas en prenant en compte toutes les valeurs de la variable, mais en écartant un certain pourcentage des valeurs situées à l’extrémité basse et à l’extrémité haute du classement des valeurs de la variable. Cette procédure consiste à pouvoir calculer une moyenne qui ne serait pas influencée par des outliers. Pour pouvoir caculer une moyenne rognée, il faut à nouveau utiliser la fonction mean(), en précisant cette fois l’argument trim avec la valeur du pourcentage de données que l’on veut rogner aux extrémités de la variable :

mean(x = iris$Sepal.Length, trim = 0.05)

Dans l’exemple de code précédent, la fonction a été configurée pour rogner 5 % des observations situées à chaque extrémité de la variable (i.e., les observations en-dessous du 5ème percentile, et celles au-dessus du 95ème percentile). Notons que lorsque l’argument trim est mis à 0 (ce qui est son paramétrage par défaut), cela consiste à calculer la moyenne normale, et que lorsque l’argument trim est mis à 0.50, cela revient à calculer la médiane puisque la fonction supprime alors 50 % des observations de part et d’autre du milieu de la variable.

Le mode

Le mode désigne la valeur qui est la plus fréquemment retrouvée dans une variable. Il n’existe pas de fonction de base dans R pour pouvoir déterminer directement le mode et pour connaître le nombre de fois que le mode apparaît dans la variable. Toutefois, nous pouvons utiliser le package lsr crée par Danielle Navarro (2018) pour retrouver ces informations en présence d’une variable quantitative. Une fois le package lsr installé puis chargé, nous pouvons utiliser la fonction modeOf() pour déterminer le mode, et la fonction maxFreq() pour savoir à quelle fréquence revient le mode dans la variable.

library(lsr)

# Détermination du mode
modeOf(x = iris$Sepal.Length)

## [1] 5

# Détermination de la fréquence du mode
maxFreq(x = iris$Sepal.Length)

## [1] 10

Bien que cela ne soit pas le cas dans l’exemple ci-dessus, il faut comprendre qu’il est à tout à fait possible d’avoir plusieurs modes si plusieurs valeurs reviennent à des fréquences similaires dans la variable. Dans ce cas, la fonction modeOf() affichera les différentes valeurs de mode, et la fonction maxFreq() continuera de n’afficher qu’une seule valeur de fréquence puisque par définition, le mode désigne la valeur associée à la fréquence d’apparition maximale dans la variable, or il ne peut n’y avoir qu’une seule fréquence maximale… Cela signifie qu’une variable peut contenenir autant de modes que de valeurs si chaque valeur n’est représentée qu’une seule fois dans la variable. Cet inconvénient est probablement l’une des raisons pour lesquelles le mode n’est que très peu utilisé, si ce n’est jamais utilisé, pour décrire la tendance centrale d’une variable quantitative.

3.1.3 Les indices de dispersion

Les indices de dispersion permettent de rendre compte de la manière selon laquelle les observations sont étalées, ou réparties, autour des indices de position. Plusieurs statistiques sont disponibles pour caractériser la dispersion, à savoir : l’étendue, l’écart-type, et l’intervalle interquartile.

L’étendue

L’étendue est la mesure la plus simple de la dispersion des données contenues dans une variable. Elle est exprimée avec la plus petite valeur (minimum) et la plus grande valeur (maximum) observée, ou alors parfois avec la différence entre ces deux valeurs. Par exemple, dans la variable ci-dessous dont les données ont été classées en ordre croissant, le minimum est 4.5, le maximum est 20.2, et l’étendue peut être donnée par l’intervalle [4.5 – 20.2]. Pour obtenir ces différents résultats dans R, il est possible d’utiliser les fonctions min(), max(), et range(). L’amplitude de l’intervalle serait ici de : 20.2-4.5 = 15.7.

vec <- c(4.5, 7.8, 10.8, 13.9, 20.2)
min(vec)

## [1] 4.5

max(vec)

## [1] 20.2

range(vec)

## [1]  4.5 20.2

L’écart-type

L’écart-type est une statistique qui donne une idée de la mesure selon laquelle les valeurs de la variable sont éloignées de la moyenne. Pour calculer l’écart-type, il faut en réalité d’abord calculer la variance \(\sigma^2\), dont le calcul est le suivant : \[\sigma^2 = \frac{1}{N}\sum_{i=1}^{N} (X{i} - \overline{X})^2\]

Cette formule signifie que pour obtenir la variance, il faut d’abord faire la somme des carrés des différences entre chaque valeur et la moyenne de la variable. Cela fait, la variance s’obtient en divisant cette somme de carrés par le nombre \(N\) de valeurs de la variable. L’écart-type \(\sigma\), c’est alors la racine carrée de la variance : \[\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N} (X{i} - \overline{X})^2}\]

Ces calculs sont valides lorsque l’on a en sa possession les données de toute la population que l’on souhaite étudier. Toutefois, lorsque l’on a en sa possession des données issues seulement d’un échantillon de la population, ces calculs biaisent les estimations de la variance et de l’écart-type correspondant à la population étudiée. Cette notion de biais traduit le fait que lorsqu’on répète un grand nombre de fois le calcul de la variance et de l’écart-type à partir, à chaque fois, d’échantillons de population différents, on a en moyenne un décalage entre la valeur de l’estimation et la réelle valeur de la variance et de l’écart-type de la population. Ce décalage systématique est tel qu’il convient dans ce cas là de diviser la somme des carrés des différences (\(X{i} - \overline{X}\)) par \(N-1\) plutôt que par \(N\) (Grenier, 2007). La formule de l’écart-type non biaisé, noté \(\hat{\sigma}\), est alors la suivante : \[\hat{\sigma} = \sqrt{\frac{1}{N-1}\sum_{i=1}^{N} (X{i} - \overline{X})^2}\]

L’écart-type est la mesure de dispersion classiquement associée à la moyenne. Si, pour un échantillon, on note une moyenne \(\overline{X}\) et un écart-type \(\hat{\sigma}\), alors le résumé d’une variable à l’aide de ces statistiques s’écrit comme suit : \(\overline{X}\) ± \(\hat{\sigma}\). Lorsque l’écart-type est divisé par la moyenne arithmétique de la variable, on obtient une valeur appelée coefficient de variation. Avec le logiciel R, les fonctions pour calculer la variance et l’écart-type non biaisés sont respectivement var() et sd().

vec <- c(4.5, 7.8, 10.8, 13.9, 20.2)
var(x = vec)

## [1] 36.153

sd(x = vec)

## [1] 6.012736

L’intervalle interquartile

L’intervalle interquartile désigne l’étendue entre le premier quartile (Q1) et le troisième quartile (Q3) d’une variable. Comme expliqué auparavant dans le cadre de la boîte à moustaches, Q1 et Q3 désignent respectivement les valeurs en-dessous desquelles 25 % et 75 % des observations de la variable se trouvent (Chatellier & Durieux, 2003). Pour un échantillon de taille \(N\), la procédure classique pour calculer les quartiles est différente selon que le rapport \(N\) / 4 est un nombre entier ou non. Lorsque ce rapport n’est pas un nombre entier, Q1 est la valeur correspondant au rang immédiatement supérieur à \(N\) / 4. Par exemple, pour la variable ci-dessous, qui a une taille \(N\) de 5 valeurs, le rapport \(N\) / 4 est égal à 1.25. Q1 est donc la valeur correspondant au rang directement supérieur, c’est-à-dire au rang 2, qui est ici la valeur 7.8.

##    1    2    3    4    5 
##  4.5  7.8 10.8 13.9 20.2

Lorsque le rapport \(N\) / 4 est un nombre entier, Q1 correspond à la moyenne des valeurs associées respectivement aux rangs \(N\) / 4 et (\(N\) / 4) + 1. Par exemple, pour la variable ci-dessous, qui a une taille \(N\) de 8 valeurs, le rapport \(N\) / 4 est à égal 2. Q1 est donc la moyenne des valeurs correspondant au rang 2 et au rang 3 (i.e., les valeurs 7.8 et 10.8), qui équivaut ici à 9.3.

##    1    2    3    4    5    6    7    8 
##  4.5  7.8 10.8 13.9 20.2 25.6 37.5 43.9

La démarche demeure la même pour déterminer Q3, à ceci près qu’on utilise le nombre 3\(N\) et non plus le nombre \(N\) pour les calculs (Labreuche, 2010). Cette méthode de calcul est en principe à privilégier en présence d’une variable discrète. Si l’on souhaite obtenir les quartiles selon cette méthode avec le logiciel R, il faut utiliser la fonction quantile() de la manière suivante :

quantile(x = vec, probs = c(0.25, 0.75), type = 2)

##   25%   75% 
##  9.30 31.55

On remarque ici que la fonction quantile() a plusieurs arguments. L’argument probs désigne les quantiles que l’on souhaite obtenir. Le quantile 0.25 correspond à Q1, et le quantile 0.75 correspond à Q3. L’argument type permet de configurer le type de calcul à effectuer pour obtenir les valeurs des quantiles recherchés. L’indication du chiffre 2 pour l’argument type permet d’obtenir les quantiles selon la méthode de calcul présentée ci-dessus, qui, comme nous l’avons précisé, est dédiée à l’étude d’une variable quantitative discrète. Par défaut, en revanche, la fonction quantile() utilise le chiffre 7 pour l’argument type, ce qui renvoie à une méthode de calcul des quantiles qui serait davantage pertinente pour étudier des variables quantitatives continues. Comparons les résultats obtenus avec les deux méthodes de calcul :

``` ```{=html}

(\#tab:quantilesCompaMethods)Comparaison des quantiles obtenus selon différentes configurations de la fonction quantile()
Quantile	Type 2	Type 7
0.25	9.30	10.050
0.75	31.55	28.575

On remarque que les résultats de la fonction quantile() sont différents selon la configuration de l’argument type. Le choix de la configuration est donc important. Pour comprendre comment R a calculé les valeurs associées aux quantiles 0.25 et 0.75 dans le cadre de la seconde méthode (i.e., avec type = 7), regardons le tableau ci-dessous.

``` ```{=html}

(\#tab:quantilesContinuousMethod)Quantiles d'une variable quantitative continue
Rang	Quantile	Valeur
1	0.0000000	4.5
2	0.1428571	7.8
3	0.2857143	10.8
4	0.4285714	13.9
5	0.5714286	20.2
6	0.7142857	25.6
7	0.8571429	37.5
8	1.0000000	43.9

Le tableau montre les données sur lesquelles R s’est appuyé pour déterminer les valeurs des quantiles recherchés (i.e., les quantiles 0.25 et 0.75 pour Q1 et Q3, respectivement). Les données du tableau sont bien celles relatives à notre variable vec, dont on peut reconnaître les valeurs dans la colonne de droite du tableau. La colonne “Quantile” montre les fractions (ou portions) de la variable vec associées aux valeurs de la variable compte tenu de leurs rangs respectifs. Par exemple, la valeur 25.6, dont le rang est 6, correspond au quantile 0.71 (approximativement). Cela veut dire que 71 % des observations ont une valeur inférieure ou égale à 25.6. Il faut savoir qu’il existe en réalité plusieurs manières de déterminer la valeur du quantile que représente chaque valeur. Dans le cas présent, le quantile représenté, que l’on va noter q, a été déterminé selon la formule suivante : \[q = (k - 1 ) / (N - 1)\] Dans le calcul ci-dessus, k désigne le rang de la valeur considérée, et \(N\) désigne la taille de la variable étudiée (i.e., le nombre total de valeurs). Comme on peut le voir dans le tableau ci-dessus, cette méthode de calcul conduit nécessairement à attribuer le quantile 0 à la valeur de rang 1, et la quantile 1 à la valeur de rang \(N\). Lorsque le nombre de valeurs fait que les quantiles 0.25 et 0.75 n’existent pas, R réalise une interpolation de la valeur correspondant au quantile recherché, cela à partir des quantiles qui existent et qui encadrent le quantile recherché, ainsi qu’à partir des valeurs correspondant à ces quantiles. Dans le cas présent, il s’agit plus précisément d’une interpolation linéaire. Voyons sur la Figure 3.10 en quoi cela consiste.

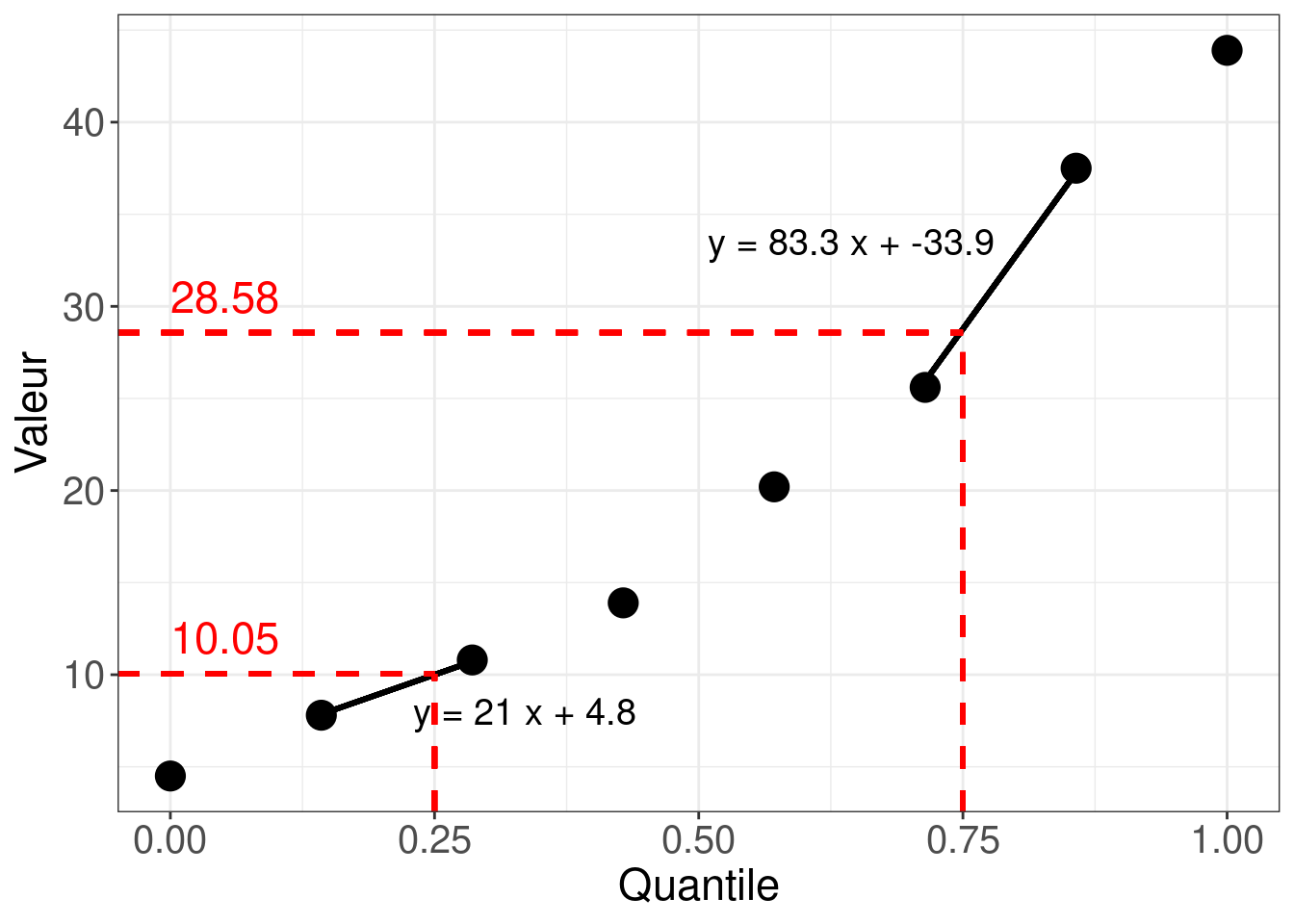
Figure 3.10: Détermination des quartiles Q1 et Q3 avec une variable quantitative continue

La figure représente les valeurs de la variable en fonction des quantiles qui leur correspondent. Les segments de couleur noire montrés sur la figure représentent les droites d’équation utilisées pour le calcul des valeurs correspondant aux quantiles 0.25 (Q1) et 0.75 (Q3), qui ne sont pas représentés initialement dans la variable étudiée. Ces droites d’équation relient les points dont les abscisses sont celles qui encadrent directement les quantiles recherchés. Ainsi, pour trouver la valeur correspondant au quantile 0.25, il a suffi de résoudre l’équation y = 21x + 4.8, en remplaçant x par 0.25. De manière analogue, pour trouver la valeur correspondant au quantile 0.75, il a suffi de résoudre l’équation y = 83.3x - 33.9 en remplaçant x par 0.75. Les solutions de ces équations sont montrées en rouge sur la partie gauche de la figure. On retrouve bien les valeurs associées aux quantiles recherchés et qui avaient été initialement obtenues avec la configuration par défaut de la fonction quantile().

Les quartiles Q1 et Q3 sont les mesures de dispersion classiquement associées à la médiane. Si on note une médiane m et l’intervalle interquartile (Q1 - Q3), alors le résumé d’une variable à l’aide de ces statistiques s’écrit comme suit : m (Q1 - Q3).

3.1.4 Les indices d’asymétrie et d’aplatissement

Le coefficient d’asymétrie (skewness)

Le fait qu’une distribution soit asymétrique désigne le fait que les observations sont réparties de manière inégale de part et d’autre du milieu de la distribution. L’indice statistique qui permet de rendre compte du niveau d’asymétrie est le coefficient d’asymétrie, ou skewness en anglais. Ce coefficient peut être obtenu à l’aide de la fonction skewness() du package e1071, qui n’existe pas dans la base de R et qu’il convient d’installer et de charger pour l’utiliser.

library(e1071)
skewness(x = iris$Sepal.Width, type = 3)

## [1] 0.3126147

Comme on peut le voir dans l’aide associée à la fonction skewness(), il existe en réalité plusieurs méthodes de calcul du coefficient d’asymétrie (noté \(\gamma_{1}\) ci-dessous). La méthode de type 3, qui est celle configurée par défaut pour cette fonction, consiste à faire le calcul suivant :

\[\gamma_{1} = \frac{1}{\hat{\sigma}^3} {\frac{\sum_{i=1}^{N} (X{i} - \overline{X})^3}{N}}\] Dans ce calcul, \(\hat{\sigma}\) désigne l’écart-type non biaisé de la variable, et \(N\) désigne la taille de la variable. Avec cette méthode, on obtient un coefficient négatif lorsque la distribution est asymétrique à gauche (longue queue vers la gauche), un coefficient de 0 lorsque la distribution est parfaitement symétrique, et un coefficient positif lorsque la distribution est asymétrique à droite (longue queue vers la droite). Ceci est illustré sur la Figure 3.11.

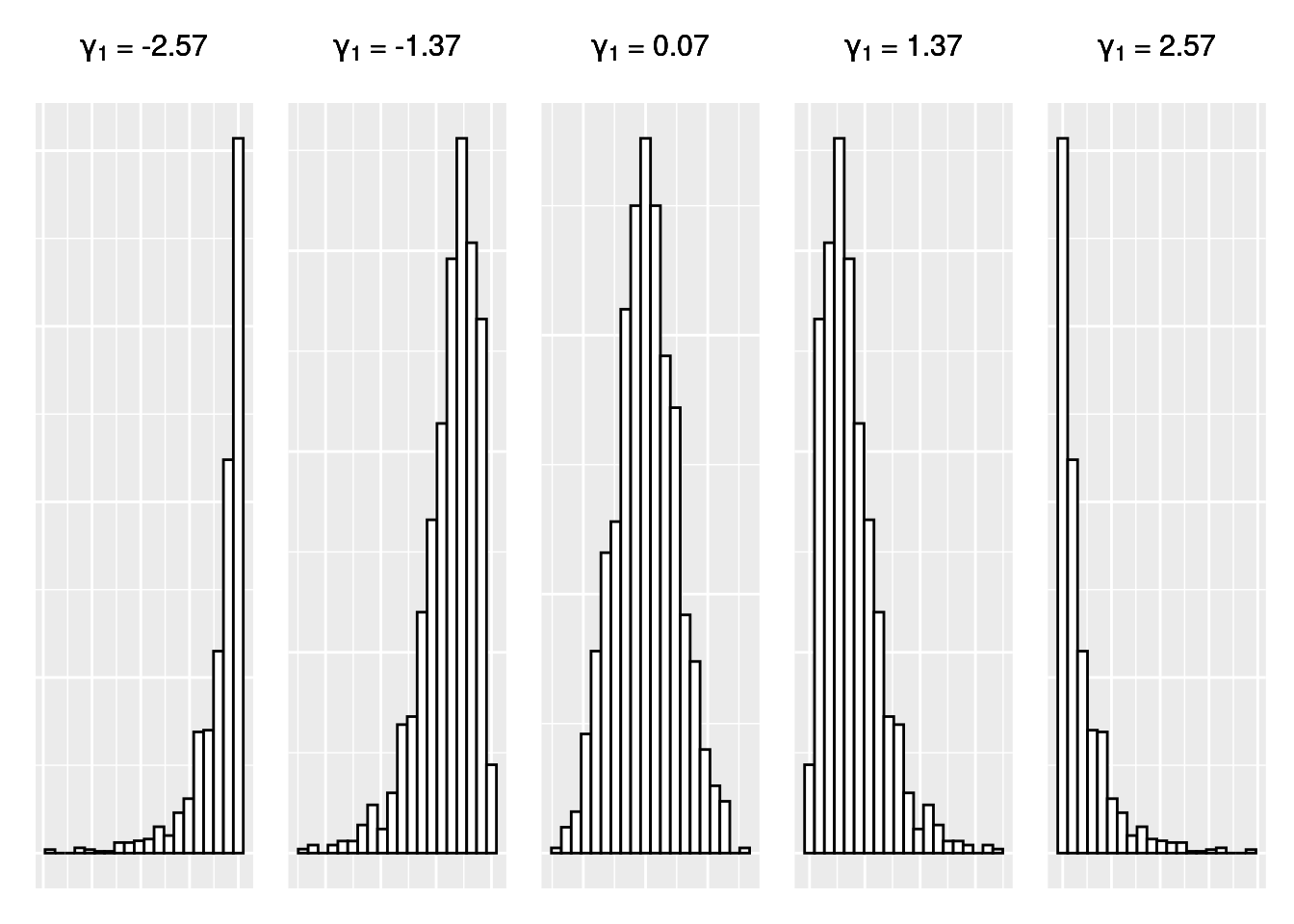
Figure 3.11: Valeur du Skewness selon la forme de la distribution

Pour aller plus loin… Joanes et Gill (1998) ont montré que lorsqu’il s’agit d’estimer le degré d’asymétrie de la distribution relative à la population étudiée, et cela à partir de l’échantillon observé, certaines méthodes de calcul du coefficient d’asymétrie peuvent être plus fiables que d’autres.

Dans le cas où la distribution des valeurs dans la population étudiée suivrait une loi normale, la méthode par défaut présentée ci-dessus serait la plus fiable pour estimer le niveau d’asymétrie lorsque l’échantillon observé est de petite taille (\(N\) < 50). Cependant, avec des échantillons de grande taille, les méthodes se valeraient.

Dans le cas où la distribution des valeurs de la population étudiée ne suivrait pas une loi normale, et qu’elle s’avèrerait très asymétrique, la méthode de type 2 proposée avec la fonction skewness() serait la plus fiable, particulièrement en présence d’échantillons de petite taille.

Le coefficient d’applatissement (kurtosis)

Le fait qu’une distribution soit aplatie désigne le fait que la forme de la distribution présente une courbure relativement plate avec des queues de distribution relativement courtes. On parle alors de distribution platycurtique. À l’inverse, lorsque la distribution est pointue avec des queues plus longues, on parle de distribution leptocurtique. L’indice statistique qui permet de rendre compte du degré d’aplatissement est le coefficient d’aplatissement, ou kurtosis en anglais. Ce coefficient peut être obtenu à l’aide de la fonction kurtosis() du package e1071.

library(e1071)
kurtosis(x = iris$Sepal.Width, type = 3)

## [1] 0.1387047

Comme on peut le voir dans l’aide associée à la fonction kurtosis(), il existe en réalité plusieurs méthodes de calcul du coefficient d’aplatissement (noté \(\gamma_{2}\) ci-dessous). La méthode de type 3, qui est celle configurée par défaut pour cette fonction, consiste à faire le calcul suivant :

\[\gamma_{2} = \frac{1}{\hat{\sigma}^4} {\frac{\sum_{i=1}^{N} (X{i} - \overline{X})^4}{N}} -3\] Dans ce calcul, \(\hat{\sigma}\) désigne l’écart-type non biaisé de la variable, et \(N\) désigne la taille de la variable. Avec cette méthode, on obtient un coefficient négatif lorsque la distribution est particulièrement aplatie par rapport à une distribution suivant une loi normale (distribution platycurtique), un coefficient de 0 lorsque la distribution suit une loi normale (distribution mésocurtique), et un coefficient positif lorsque la distribution est particulièrement pointue par rapport à une loi normale (distribution leptocurtique). Ceci est illustré sur la Figure 3.12.

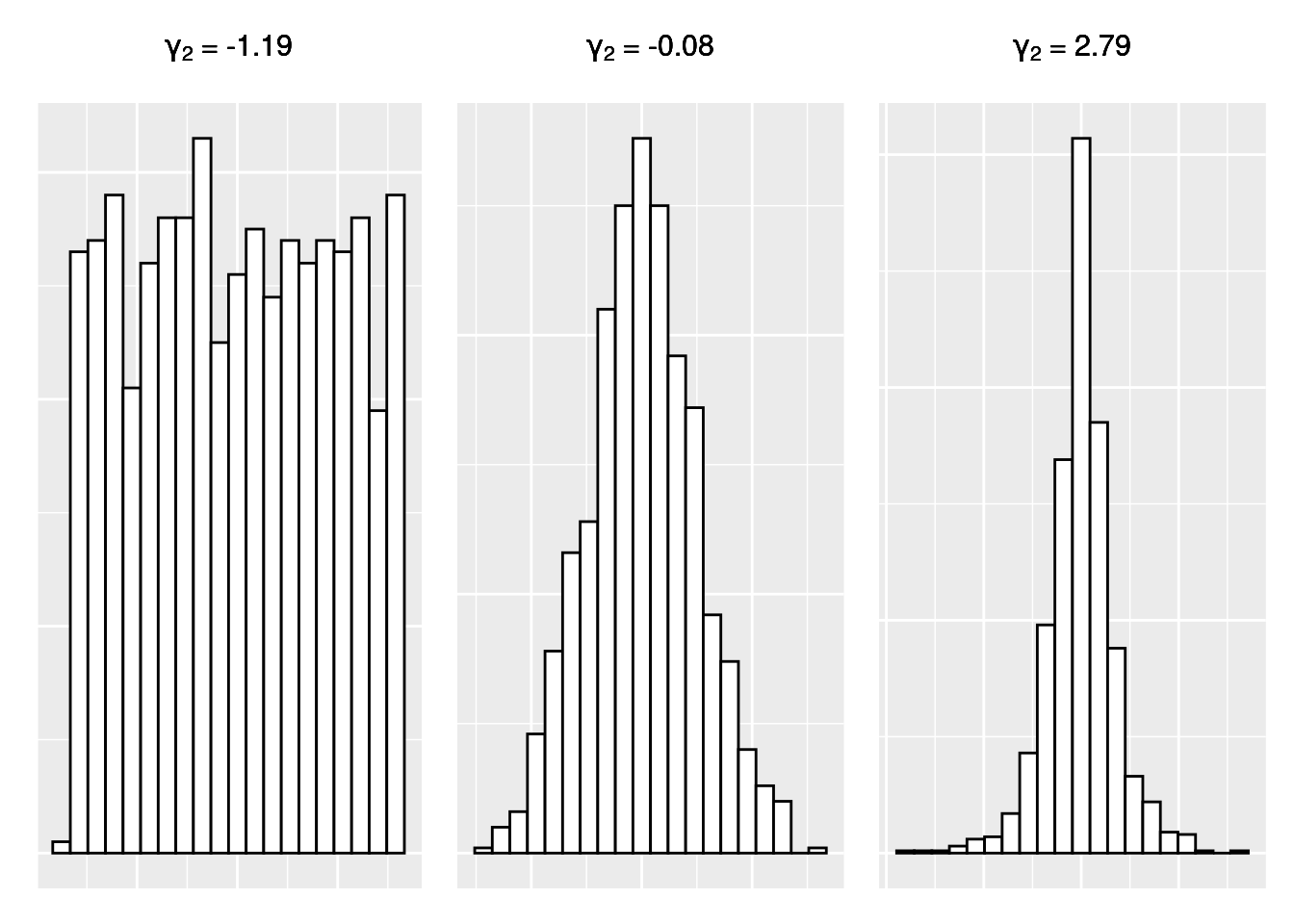
Figure 3.12: Valeur du Kurtosis selon la forme de la distribution

Pour aller plus loin… Comme avec le coefficient d’asymétrie, Joanes et Gill (1998) ont montré que lorsqu’il s’agit d’estimer le degré d’aplatissement de la distribution relative à la population étudiée, et cela à partir de l’échantillon observé, certaines méthodes de calcul du coefficient d’aplatissement peuvent être plus fiables que d’autres.

Dans le cas où la distribution des valeurs dans la population étudiée suivrait une loi normale, la méthode de type 1 proposée avec la fonction kurtosis() serait la plus fiable pour estimer le niveau d’aplatissement lorsque l’échantillon observé est de petite taille (\(N\) < 50). Cependant, la méthode par défaut présentée plus haut fournirait des résultats relativement proches de ceux obtenus avec la méthode de type 1. De plus, avec des échantillons de grande taille, toutes les méthodes se valeraient.

Dans le cas où la distribution des valeurs de la population étudiée ne suivrait pas une loi normale, et s’avèrerait très asymétrique, la méthode de type 2 proposée avec la fonction kurtosis() serait la plus fiable, particulièrement en présence d’échantillons de petite taille.

3.1.5 Fonctions pour obtenir un récapitulatif des statistiques descriptives

Il existe plusieurs fonctions pour avoir une vue d’ensemble des statistiques généralement utilisées pour explorer et résumer une variable quantitative. Une fonction particulièrement intéressante est la fonction describe() du package psych.

library(psych)

La fonction describe() peut être utilisée sur une variable donnée :

psych::describe(x = iris$Sepal.Width, quant = c(0.25, 0.75))

##    vars   n mean   sd median trimmed  mad min max range skew kurtosis
## X1    1 150 3.06 0.44      3    3.04 0.44   2 4.4   2.4 0.31     0.14
##      se Q0.25 Q0.75
## X1 0.04   2.8   3.3

La fonction describe() peut être aussi utilisée sur un jeu de données entier. (Attention, les résumés numériques fournis pour les variables qualitatives n’auront pas de sens ; les variables qualitatives détectées sont indiquées avec un astérisque dans le tableau de résultats.)

psych::describe(x = iris, quant = c(0.25, 0.75))

##              vars   n mean   sd median trimmed  mad min max range
## Sepal.Length    1 150 5.84 0.83   5.80    5.81 1.04 4.3 7.9   3.6
## Sepal.Width     2 150 3.06 0.44   3.00    3.04 0.44 2.0 4.4   2.4
## Petal.Length    3 150 3.76 1.77   4.35    3.76 1.85 1.0 6.9   5.9
## Petal.Width     4 150 1.20 0.76   1.30    1.18 1.04 0.1 2.5   2.4
## Species*        5 150 2.00 0.82   2.00    2.00 1.48 1.0 3.0   2.0
##               skew kurtosis   se Q0.25 Q0.75
## Sepal.Length  0.31    -0.61 0.07   5.1   6.4
## Sepal.Width   0.31     0.14 0.04   2.8   3.3
## Petal.Length -0.27    -1.42 0.14   1.6   5.1
## Petal.Width  -0.10    -1.36 0.06   0.3   1.8
## Species*      0.00    -1.52 0.07   1.0   3.0

On retrouve la plupart des statistiques que nous avons vues jusqu’à présent, notamment le skewness et le kurtosis qui ont été ici calculés avec la méthode par défaut du package e1071. Pour changer la méthode de calcul de ces deux coefficients, il suffit de modifier l’argument type de la fonction, comme dans le cadre de l’utilisation du package e1071 et des fonctions skewness() et kurtosis() associées. On notera cependant qu’il ne semble pas possible de modifier la méthode de calcul des quantiles, qui sont ici calculés selon la méthode par défaut configurée telle qu’avec la fonction quantile().

Enfin, il est aussi possible d’obtenir ces récapitulatifs numériques en fonction des modalités d’une variable qualitative du jeu de données, grâce à la fonction describeBy() du package psych. Dans l’exemple ci-dessous, la variable qualitative est indiquée grâce à l’argument group.

psych::describeBy(x = iris, quant = c(0.25, 0.75), group = iris$Species)

## 
##  Descriptive statistics by group 
## group: setosa
##              vars  n mean   sd median trimmed  mad min max range skew
## Sepal.Length    1 50 5.01 0.35    5.0    5.00 0.30 4.3 5.8   1.5 0.11
## Sepal.Width     2 50 3.43 0.38    3.4    3.42 0.37 2.3 4.4   2.1 0.04
## Petal.Length    3 50 1.46 0.17    1.5    1.46 0.15 1.0 1.9   0.9 0.10
## Petal.Width     4 50 0.25 0.11    0.2    0.24 0.00 0.1 0.6   0.5 1.18
## Species         5 50 1.00 0.00    1.0    1.00 0.00 1.0 1.0   0.0  NaN
##              kurtosis   se Q0.25 Q0.75
## Sepal.Length    -0.45 0.05   4.8  5.20
## Sepal.Width      0.60 0.05   3.2  3.68
## Petal.Length     0.65 0.02   1.4  1.58
## Petal.Width      1.26 0.01   0.2  0.30
## Species           NaN 0.00   1.0  1.00
## ---------------------------------------------------- 
## group: versicolor
##              vars  n mean   sd median trimmed  mad min max range
## Sepal.Length    1 50 5.94 0.52   5.90    5.94 0.52 4.9 7.0   2.1
## Sepal.Width     2 50 2.77 0.31   2.80    2.78 0.30 2.0 3.4   1.4
## Petal.Length    3 50 4.26 0.47   4.35    4.29 0.52 3.0 5.1   2.1
## Petal.Width     4 50 1.33 0.20   1.30    1.32 0.22 1.0 1.8   0.8
## Species         5 50 2.00 0.00   2.00    2.00 0.00 2.0 2.0   0.0
##               skew kurtosis   se Q0.25 Q0.75
## Sepal.Length  0.10    -0.69 0.07  5.60   6.3
## Sepal.Width  -0.34    -0.55 0.04  2.52   3.0
## Petal.Length -0.57    -0.19 0.07  4.00   4.6
## Petal.Width  -0.03    -0.59 0.03  1.20   1.5
## Species        NaN      NaN 0.00  2.00   2.0
## ---------------------------------------------------- 
## group: virginica
##              vars  n mean   sd median trimmed  mad min max range
## Sepal.Length    1 50 6.59 0.64   6.50    6.57 0.59 4.9 7.9   3.0
## Sepal.Width     2 50 2.97 0.32   3.00    2.96 0.30 2.2 3.8   1.6
## Petal.Length    3 50 5.55 0.55   5.55    5.51 0.67 4.5 6.9   2.4
## Petal.Width     4 50 2.03 0.27   2.00    2.03 0.30 1.4 2.5   1.1
## Species         5 50 3.00 0.00   3.00    3.00 0.00 3.0 3.0   0.0
##               skew kurtosis   se Q0.25 Q0.75
## Sepal.Length  0.11    -0.20 0.09  6.23  6.90
## Sepal.Width   0.34     0.38 0.05  2.80  3.18
## Petal.Length  0.52    -0.37 0.08  5.10  5.88
## Petal.Width  -0.12    -0.75 0.04  1.80  2.30
## Species        NaN      NaN 0.00  3.00  3.00

Notons aussi l’existence de la fonction skim() du package skimr pour obtenir un résumé clair des types de variables et des statistiques principales, ainsi que des valeurs manquantes :

library(skimr)

# Analyse de l'ensemble des variables
skim(iris)

Tableau 3.1: Data summary
Name	iris
Number of rows	150
Number of columns	5
_______________________
Column type frequency:
factor	1
numeric	4
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
Species	0	1	FALSE	3	set: 50, ver: 50, vir: 50

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
Sepal.Length	1	5.84	0.83	4.3	5.1	5.80	6.4	7.9	▆▇▇▅▂
Sepal.Width	1	3.06	0.44	2.0	2.8	3.00	3.3	4.4	▁▆▇▂▁
Petal.Length	1	3.76	1.77	1.0	1.6	4.35	5.1	6.9	▇▁▆▇▂
Petal.Width	1	1.20	0.76	0.1	0.3	1.30	1.8	2.5	▇▁▇▅▃

# Analyse d'une variable (Sepal.Length) par groupe (Species)
iris |>
  dplyr::select(Species, Sepal.Length) |> 
  dplyr::group_by(Species) |>
  skim()

Tableau 3.1: Data summary
Name	dplyr::group_by(dplyr::se…
Number of rows	150
Number of columns	2
_______________________
Column type frequency:
numeric	1
________________________
Group variables	Species

Variable type: numeric

skim_variable	Species	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
Sepal.Length	setosa	1	5.01	0.35	4.3	4.80	5.0	5.2	5.8	▃▃▇▅▁
Sepal.Length	versicolor	1	5.94	0.52	4.9	5.60	5.9	6.3	7.0	▂▇▆▃▃
Sepal.Length	virginica	1	6.59	0.64	4.9	6.23	6.5	6.9	7.9	▁▃▇▃▂

3.1.6 Quelles statistiques choisir pour résumer une variable quantitative dans un rapport ?

Les statistiques les plus couramment utilisées pour résumer une variable quantitative sont les paramètres de position (moyenne et médiane principalement) en lien avec les paramètres de dispersion correspondants. Aucun paramètre de position ne surpasse les autres dans toutes les situations. Le choix du paramètre de position, en lien avec le paramètre de dispersion associé, dépend de l’objectif de l’analyse.

Lorsqu’il s’agit de simplement décrire une distribution des données obtenues à titre exploratoire, certains auteurs proposent d’utiliser les trois paramètres de position (moyenne, médiane, mode), en sachant que la médiane, d’un point de vue purement descriptif, peut être le paramètre le plus adapté dans de nombreuses situations (Gonzales & Ottenbacher, 2001). Dans le cas où la distribution s’avèrerait plutôt gaussienne, la moyenne et l’écart-type sont intéressants car dans ce cas, on sait que :

Approximativement 68.3 % des observations sont comprises dans l’intervalle [\(\overline{X}\) - 1 \(\hat{\sigma}\) ; \(\overline{X}\) + 1 \(\hat{\sigma}\)],
Approximativement 95.5 % des observations sont comprises dans l’intervalle [\(\overline{X}\) - 2 \(\hat{\sigma}\) ; \(\overline{X}\) + 2 \(\hat{\sigma}\)],
Approximativement 99.7 % des observations sont comprises dans l’intervalle [\(\overline{X}\) - 3 \(\hat{\sigma}\) ; \(\overline{X}\) + 3 \(\hat{\sigma}\)].

Ceci est illustré sur la Figure 3.13.

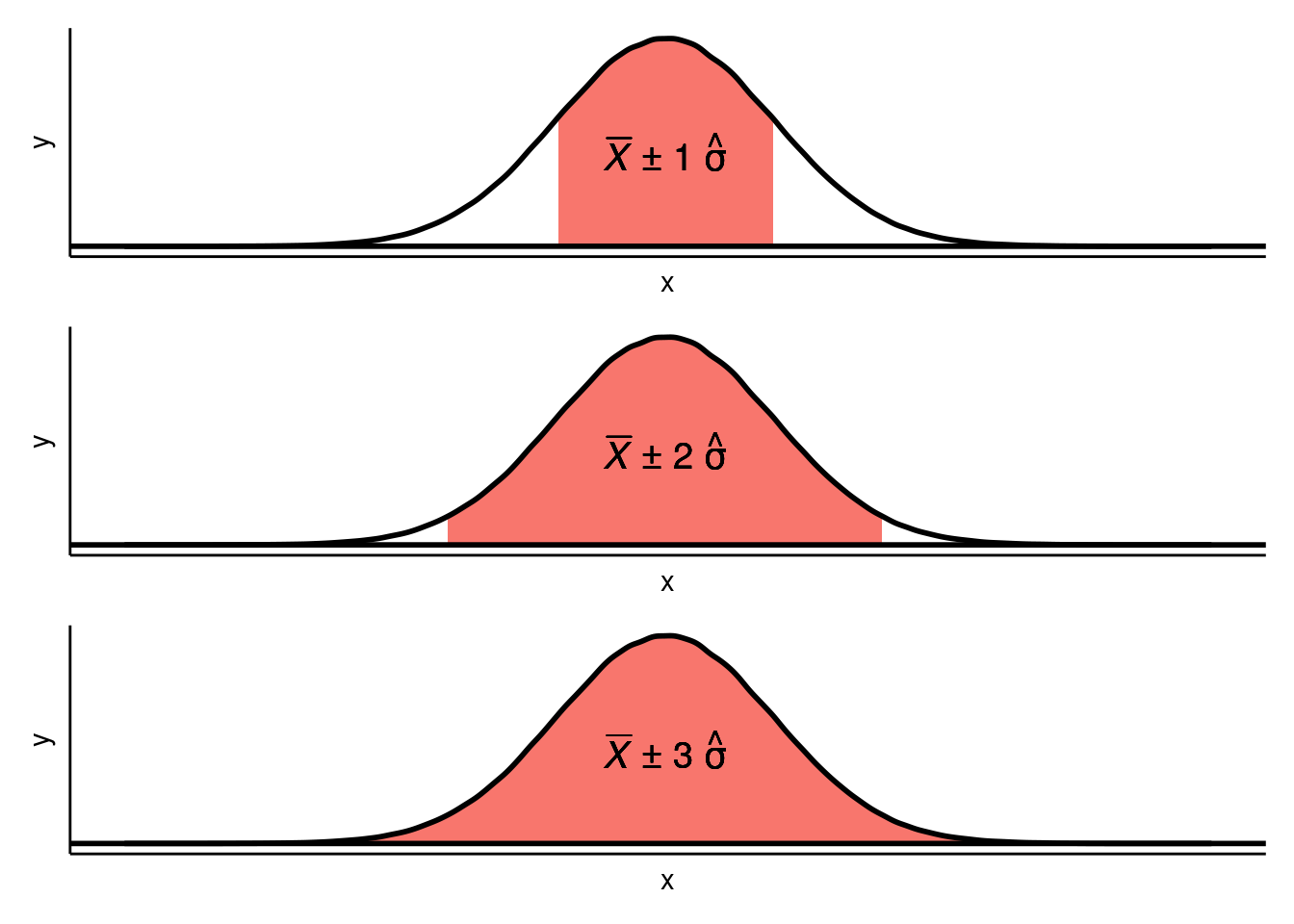
Figure 3.13: Proportions des observations incluses dans différents intervalles liés à la moyenne et à des multiples de l’écart-type

Lorsqu’il s’agit plus précisément de vouloir renseigner sur la tendance centrale relative à l’échantillon étudié, le choix dépend de la forme de la distribution observée. Lorsque la distribution est gaussienne, la moyenne, la médiane, et le mode, sont similaires et donc se valent. Toutefois, lorsque la distribution est asymétrique et unimodale (i.e., avec un seul pic), le mode reflètera mieux la tendance centrale. De plus, lorsque la distribution est asymétrique, la médiane aura tendance à mieux représenter la tendance centrale que la moyenne (Rousselet & Wilcox, 2020). Notons que dans certains cas où la distribution semble asymétrique, la médiane peut se retrouver malgré tout plus éloignée du mode que la moyenne, comme illustré dans l’exemple emprunté à Gonzales et al. (2001) qui est montré sur la Figure 3.14.

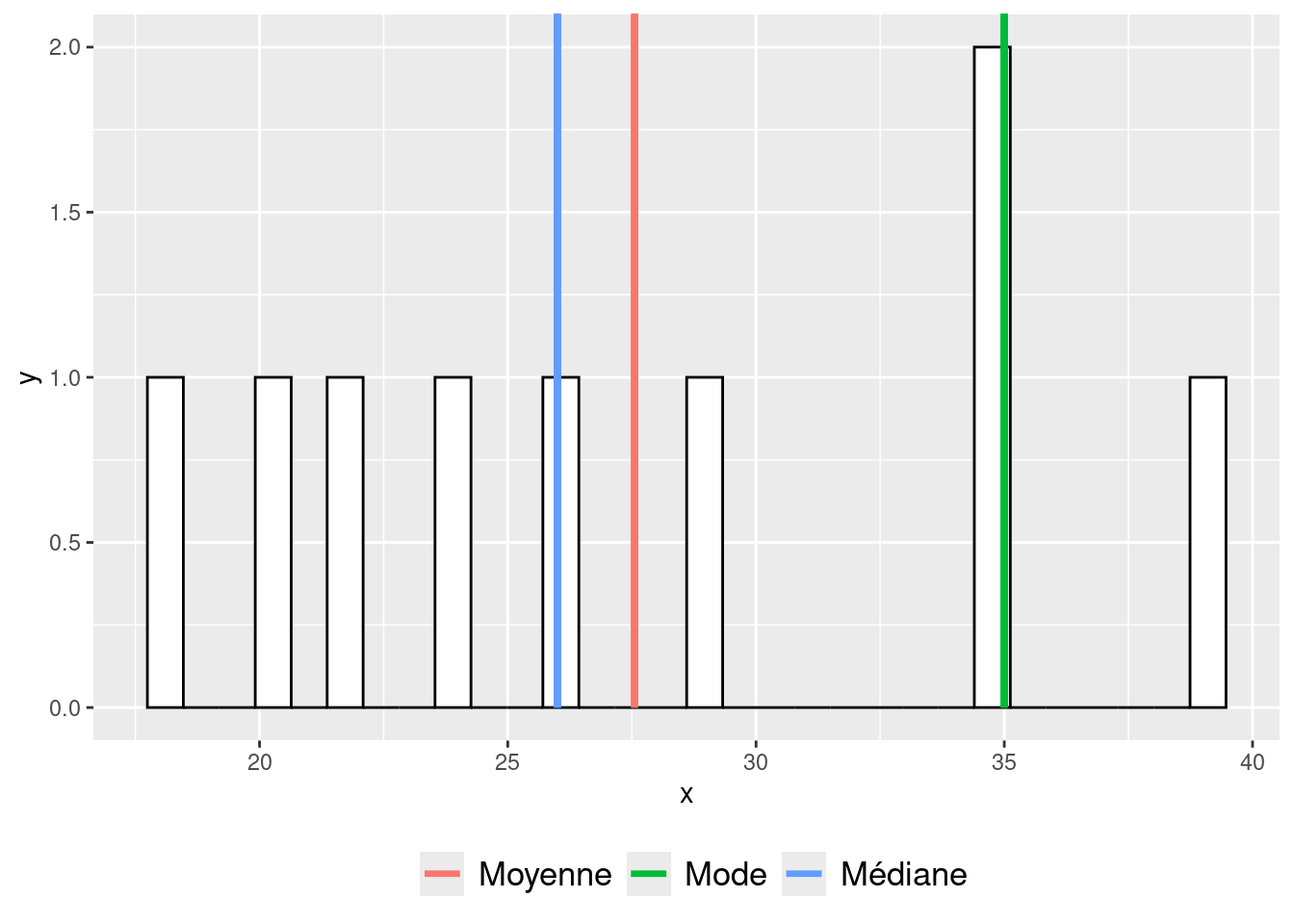
Figure 3.14: Exemples de positions de la moyenne et de la médiane dans le cadre d’une distribution asymétrique

3.2 Variables qualitatives

3.2.1 Visualiser la distribution de la variable

Comme dans le cadre de variables quantitatives, une bonne pratique est de visualiser graphiquement la distribution d’une variable qualitative avant de l’analyser. Ici, il s’agit plus précisément de prendre connaissance des effectifs correspondant aux différentes modalités de la variable. Une manière rapide de procéder pour cela est d’utiliser la fonction ggplot() et la fonction geom_bar(). Illustrons cela avec le jeu de données diamonds, qui contient notamment la variable qualitative color.

# Aperçu du jeu de données
diamonds

## # A tibble: 53,940 × 10
##    carat cut       color clarity depth table price     x     y     z
##    <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
##  1  0.23 Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
##  2  0.21 Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
##  3  0.23 Good      E     VS1      56.9    65   327  4.05  4.07  2.31
##  4  0.29 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
##  5  0.31 Good      J     SI2      63.3    58   335  4.34  4.35  2.75
##  6  0.24 Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48
##  7  0.24 Very Good I     VVS1     62.3    57   336  3.95  3.98  2.47
##  8  0.26 Very Good H     SI1      61.9    55   337  4.07  4.11  2.53
##  9  0.22 Fair      E     VS2      65.1    61   337  3.87  3.78  2.49
## 10  0.23 Very Good H     VS1      59.4    61   338  4     4.05  2.39
## # ℹ 53,930 more rows

# Visualisation de la distribution de la variable color
diamonds |> 
  ggplot(aes(x = color)) + 
    geom_bar()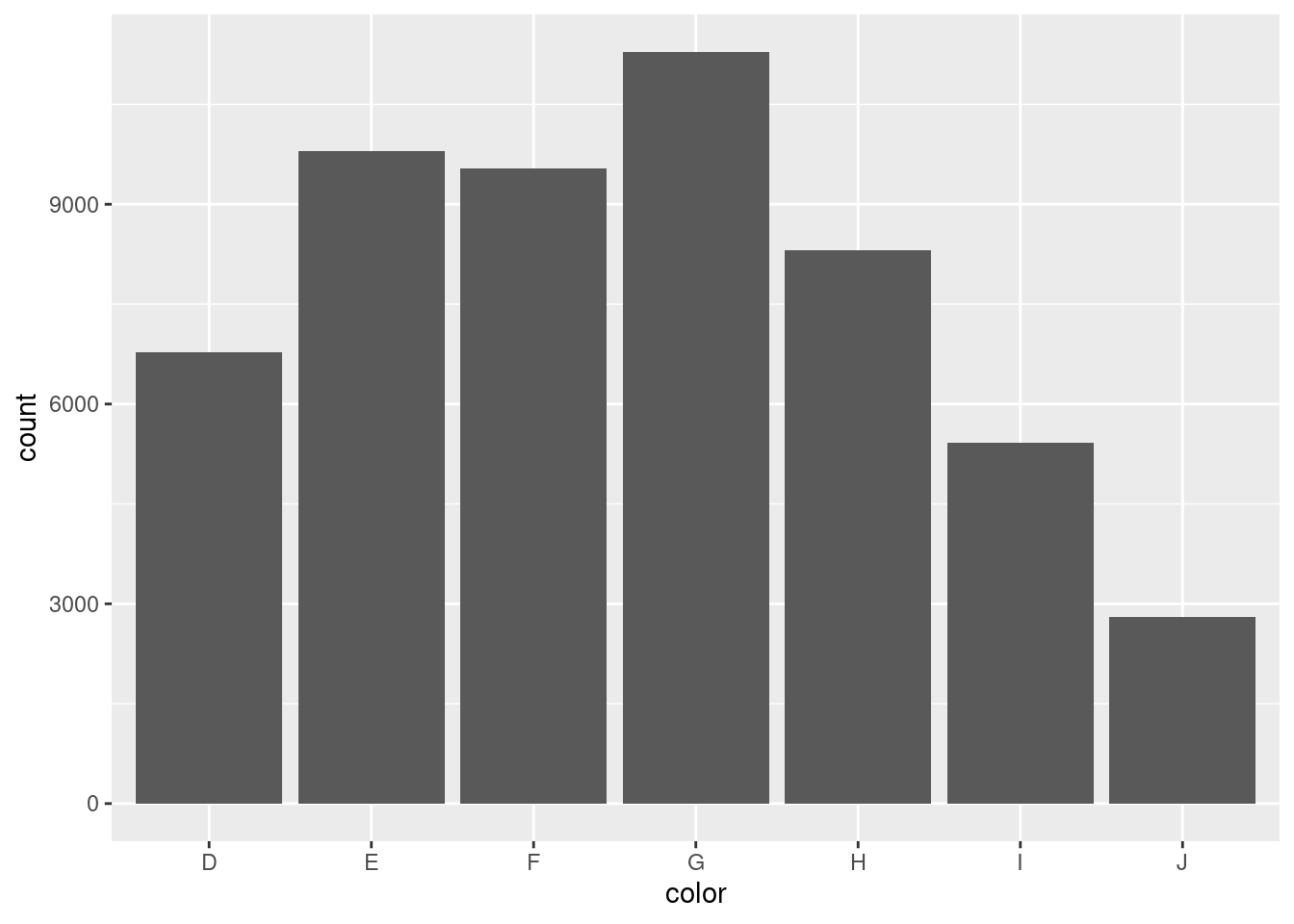

Figure 3.15: Exemple de diagramme en barres

Bien que rapide, la manière de procéder avec le code montré ci-avant devient vite limitée lorsque l’on veut enrichir le graphique, tel qu’en ajoutant les valeurs des effectifs au-dessus des barres ou encore en changeant l’ordre de disposition des barres. Pour gagner en capacité de modification du graphique, on peut d’abord passer par une étape intermédiaire consistant à créer un mini-jeu de données où la variable color serait déjà résumée à l’aide de la fonction count du package dplyr, de telle sorte à n’avoir que la valeur de l’effectif en regard de chaque modalité. Ceci est montré dans le code ci-dessous.

diamonds |> 
  count(color)

## # A tibble: 7 × 2
##   color     n
##   <ord> <int>
## 1 D      6775
## 2 E      9797
## 3 F      9542
## 4 G     11292
## 5 H      8304
## 6 I      5422
## 7 J      2808

Si l’on poursuit le code avec les fonctions ggplot() et geom_bar() (cf. code ci-dessous), on arrive alors au même résultat que précédemment (cf Figure 3.15). On note qu’il a fallu adapter l’argument stat de la fonction geom_bar() pour que le graphique montre bien en ordonnées la valeur de la variable nouvellement appelée n, qui comprend les effectifs de chaque modalité.

diamonds |> 
  count(color) |>
  ggplot(aes(x = color, y = n)) +
     geom_bar(stat = "identity")

Certes, pour le moment, cette seconde procédure n’a fait que rajouter une ligne de code par rapport à la première procédure. Toutefois, en reprenant la logique de la seconde procédure, on peut à présent créer des graphiques en barres plus élaborés relativement facilement, comme montré ci-dessous.

# Diagramme en barres avec les effectifs affichés à proximité des barres
A <- 
  diamonds |>
  count(color) |>
  ggplot(aes(x = color, y = n)) +
     geom_bar(stat = "identity") +
     geom_text(aes(label = n), size = 2, nudge_y = 700) +
     ggtitle("A")

# Diagramme en barres réorganisées manuellement
B <- 
  diamonds |>
  count(color) |>
  ggplot(aes(x = fct_relevel(color, "J", "I", "H", "G", "F", "E", "D"), 
             y = n)) +
     geom_bar(stat = "identity") +
     xlab("color") +
     ggtitle("B") 

# Diagramme en barres réorganisées en ordre croissant
C <- 
  diamonds |>
  count(color) |>
  ggplot(aes(x = fct_reorder(color, n), y = n)) +
     geom_bar(stat = "identity") +
     xlab("color") +
     ggtitle("C") 

# Diagramme en barres réorganisées en ordre décroissant
D <- 
  diamonds |>
  count(color) |>
  ggplot(aes(x = fct_reorder(color, -n), y = n)) +
     geom_bar(stat = "identity") +
     xlab("color") +
     ggtitle("D") 

# Diagramme en barres pivoté
E <- 
  diamonds |>
  count(color) |>
  ggplot(aes(x = fct_reorder(color, -n), y = n)) +
  geom_bar(stat = "identity") +
     coord_flip() +
     ggtitle("E")

# Dotplot pivoté
F <- 
  diamonds |>
  count(color) |>
  ggplot(aes(x = fct_reorder(color, -n), y = n)) +
     geom_point() +
     coord_flip() +
     ggtitle("F")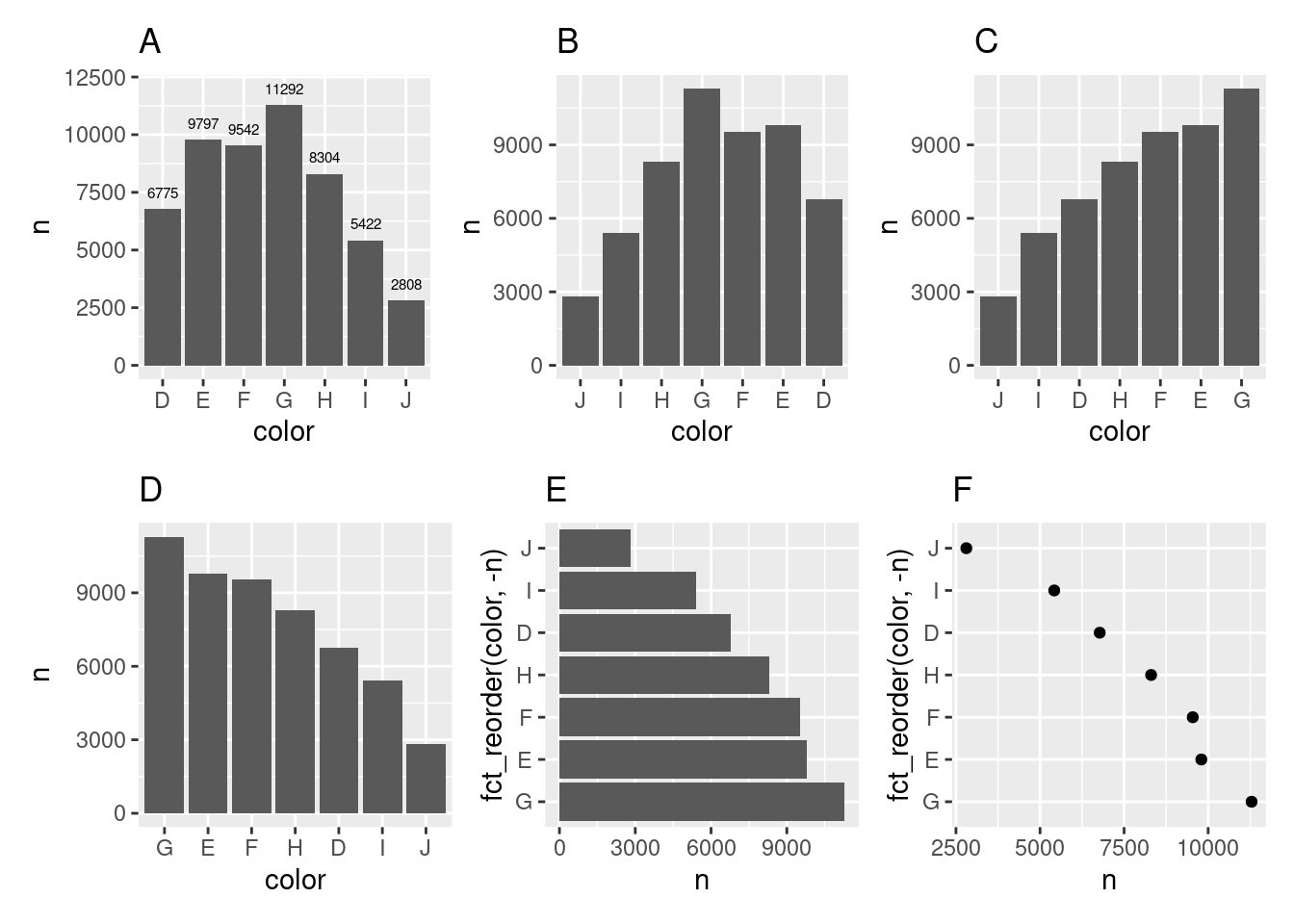

Figure 3.16: Différentes sortes de diagrammes en barres

Dans le code montré ci-dessus, on remarque que le réagencement manuel des barres (cf. graphique B) a pu être réalisé grâce à la fonction fct_relevel() du package forcats. Pour les autres diagrammes, la réorganisation des barres en ordre croissant ou décroissant sur la base de la valeur de l’effectif (n) a pu se faire grâce à la fonction fct_reorder() du package forcats. Les noms des arguments de ces fonctions n’ont pas été indiqués pour alléger le code. Le plus important, c’est d’indiquer en premier dans la fonction la variable dont l’ordre d’apparition des modalités doit être réorganisé (il s’agissait de la variable color dans cet exemple). En second, il convient d’indiquer la logique de réorganisation de l’apparition des modalités (ce qui a été fait sur la base des valeurs de la variable n dans les exemples ci-dessus utilisant la fonction fct_reorder()).

Toujours dans le code montré ci-dessus, on peut voir aussi, dans la fonction geom_text() du graphique A, la présence de l’argument nudge_y. Cet argument permet de régler le décalage entre le haut de la barre et le texte. L’unité du chiffre indiqué est celle de la variable montrée en ordonnées.

On observe que la réorganisation des barres selon un ordre croissant ou décroissant clarifie l’information délivrée par le graphique. Toutefois, cette réorganisation est en principe surtout recommandée pour des variables qualitative nominales, c’est-à-dire des variables pour lesquelles il n’existe pas un ordre naturel des modalités. Lorsqu’il existe un ordre naturel des modalités, comme c’est le cas pour des variables qualitatives ordinales, les modalités devraient préférentiellement suivre leur ordre naturel.

En plus des effectifs, il est aussi possible de prendre connaissance de la distribution à l’aide des proportions, c’est-à-dire des ratios entre les effectifs liés aux différentes modalités et l’effectif total. Les proportions peuvent être visualisées avec un diagramme circulaire (i.e., un camembert), avec un diagramme en barres empilées, ou avec des barres disposées côte-à-côte. Les diagrammes circulaires et avec barres empilées mettent en avant le fait que les parties individuelles étudiées font partie d’un même ensemble. Les diagrammes circulaires peuvent être utilisés efficacement à cet effet lorsqu’ils montrent des fractions simples telles qu’un quart, un tiers, ou une moitié. Toutefois, les parties individuelles sont plus facilement comparables lorsqu’on utilise des barres mises côte-à-côte, comme montré ci-avant. Les diagrammes avec barres empilées sont quant à eux difficiles à comprendre lorsqu’il s’agit de n’étudier qu’une seule variable qualitative (Wilke, 2018).

# Diagramme en barres empilées montrant les effectifs
A <-
  diamonds |>
  count(color) |>
  ggplot(aes(x = "", y = n, fill = color)) +
  geom_bar(stat = "identity", na.rm = TRUE) +
  geom_text(aes(label = n),
            size = 2,
            position = position_stack(vjust = 0.5)) +
  ggtitle("A")

# Diagramme en barres empilées montrant les proportions
B <-
  diamonds |>
  count(color) |>
  mutate(prop = n / sum(n) * 100) |>
  ggplot(aes(x = "", y = prop, fill = color)) +
  geom_bar(stat = "identity") +
  geom_text(aes(label = paste0(round(prop, digits = 2), " %")),
            size = 2,
            position = position_stack(vjust = 0.5)) +
  ggtitle("B")

# Diagramme circulaire montrant les effectifs
C <-
  diamonds |>
  group_by(color) |>
  summarize(n = n()) |>
  ggplot(aes(x = "", y = n, fill = color)) +
  geom_bar(stat = "identity", position = "stack") +
  coord_polar(theta = "y",
              start = 0,
              direction = -1) +
  geom_text(aes(label = n),
            size = 2,
            position = position_stack(vjust = 0.5)) +
  ggtitle("C")

# Diagramme circulaire montrant les proportions
D <-
  diamonds |>
  count(color) |>
  mutate(prop = n / sum(n) * 100) |>
  ggplot(aes(x = "", y = prop, fill = color)) +
  geom_bar(stat = "identity", position = "stack") +
  coord_polar(theta = "y",
              start = 0,
              direction = -1) +
  geom_text(aes(label = paste0(round(prop, digits = 2), " %")),
            size = 2,
            position = position_stack(vjust = 0.5)) +
  ggtitle("D")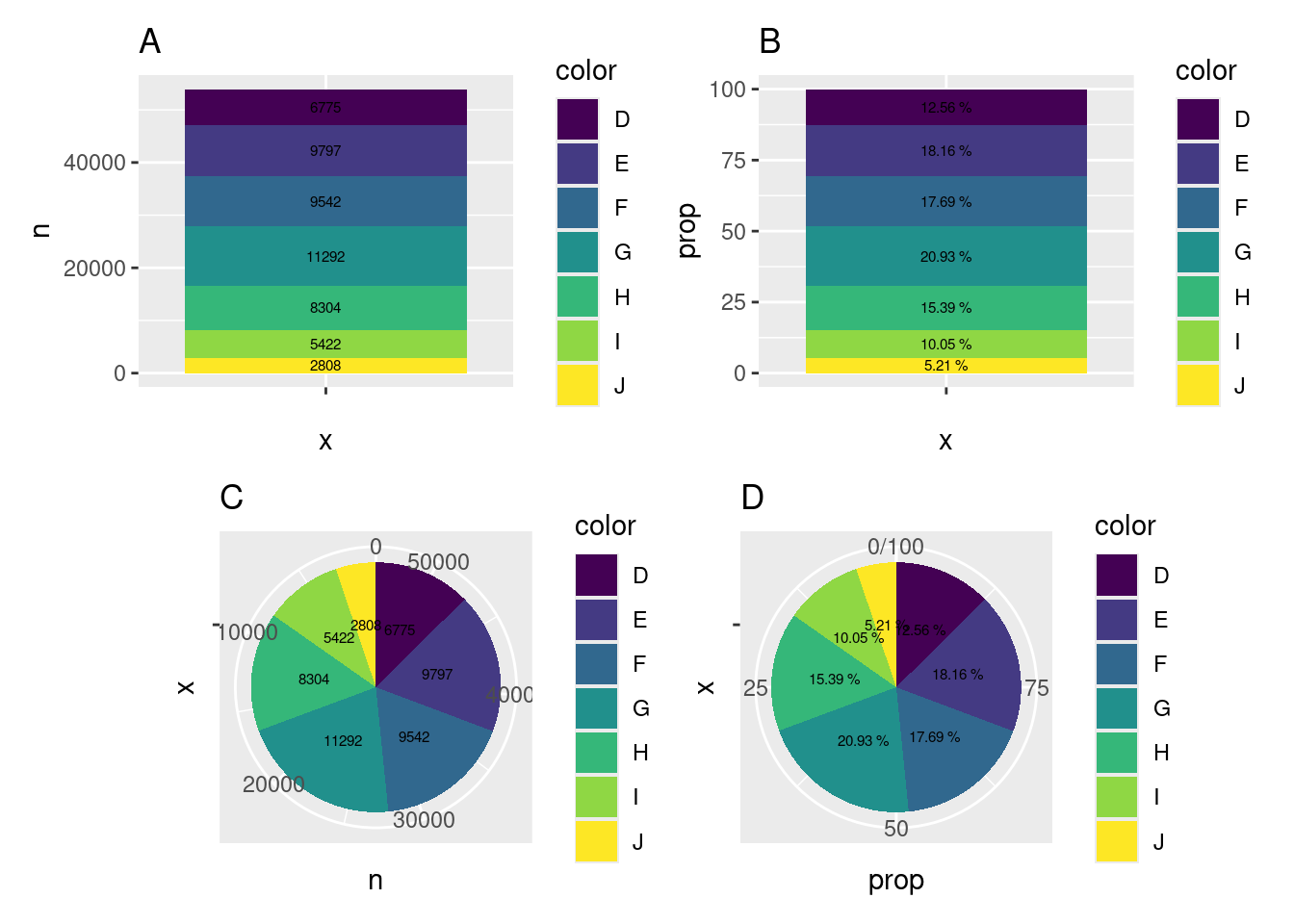

Figure 3.17: Différentes sortes de diagrammes pour représenter des proportions

3.2.2 Déterminer la tendance centrale

Dans le cadre de variables qualitatives, la tendance centrale peut être renseignée à l’aide du mode en présence d’une variable nominale, et à l’aide de la médiane ou du mode en présence d’une variable ordinale (Gonzales & Ottenbacher, 2001). Avec des variables qualitatives, il est possible de prendre connaissance du mode facilement à l’aide d’un tableau de résultats qui récapitule, par ordre décroissant, les effectifs et les proportions associées aux différentes modalités de la variable étudiée. Ce type de tableau peut être obtenu à l’aide de la fonction freq() du package questionr, qu’il convient d’installer et charger au préalable afin de pouvoir l’utiliser. Dans l’exemple ci-dessous, le mode de la variable color dans le jeu de données diamonds est la modalité présente sur la première ligne du tableau.

library(questionr)
freq(diamonds$color, valid = TRUE, total = TRUE, sort = "dec")

##           n     %  val%
## G     11292  20.9  20.9
## E      9797  18.2  18.2
## F      9542  17.7  17.7
## H      8304  15.4  15.4
## D      6775  12.6  12.6
## I      5422  10.1  10.1
## J      2808   5.2   5.2
## Total 53940 100.0 100.0

3.3 Résumé

En statistiques, la notion de population désigne l’ensemble des individus existant qui présentent un ou plusieurs critères d’intérêt. Un échantillon est alors une fraction de la population étudiée, composée d’individus qui en principe sont représentatifs de la population étudiée.
Avec R, les graphiques peuvent être réalisés, entre autres, à l’aide du package ggplot2 et des fonctions associées.
Lors de l’analyse d’une variable quantitative, une première étape doit être de visualiser graphiquement la distribution des observations. Cela peut se faire à l’aide :
- d’un histogramme avec la fonction ggplot2::geom_histogram() ;
- d’une boîte à moustaches avec la fonction ggplot2::geom_boxplot() ;
- ou encore d’un raincloud plot avec la fonction ggrain::geom_rain().
La distribution d’une variable quantitative peut être notamment de forme gaussienne, asymétrique, leptocurtique, ou encore platycurtique.
Les indices de position disponibles pour résumer une variable quantitative sont la moyenne (mean()), la médiane (median()), le mode (lsr::modeOf()), et la moyenne rognée (mean(trim = ...)).
Les indices de dispersion disponibles pour résumer une variable quantitative sont l’étendue (min(), max(), range()), l’écart-type (sd()), et les quartiles (quantile(probs = c(0.25, 0.75))).
L’indice statistique permettant de décrire le niveau d’asymétrie d’une variable quantitative est le coefficient d’asymétrie (e1071::skewness()).
L’indice statistique permettant de décrire le niveau d’aplatissement d’une variable quantitative est le coefficient d’aplatissement (e1071::kurtosis()).
Les fonctions psych::describe(), psych::describeBy() ou encore skimr::skim() permettent de récapituler les indices statistiques généralement étudiés dans le cadre de variables quantitatives.
Lorsque la distribution d’une variable quantitative est gaussienne, approximativement 68.3 %, 95.5 %, et 99.7 % des observations sont situées dans ± 1 s, ± 2 s, et ± 3 s autour de la moyenne, respectivement (s étant l’écart-type de la variable).
Lorsque la distribution d’une variable quantitative est asymétrique, la médiane peut être l’indicateur le plus adapté pour décrire la tendance centrale, en particulier en présence de petits échantillons.
Lors de l’analyse d’une variable qualitative, une première étape doit être de visualiser graphiquement la distribution des effectifs. Cela peut se faire à l’aide d’un diagramme en barres (ggplot2::geom_bar()).
Les variables qualitatives nominales devraient être visualisées avec une organisation des modalités selon un ordre croissant ou décroissant.
Les variables qualitatives ordinales devraient être visualisées avec une organisation des modalités selon leur ordre naturel.
Dans le cadre de variables qualitatives nominales, la tendance centrale peut être étudiée à l’aide du mode.
Dans le cadre de variables qualitatives ordinales, la tendance centrale peut être étudiée à l’aide de la médiane ou du mode.
La fonction questionr::freq() permet de récapituler les effectifs et les proportions relatifs aux modalités d’une variable qualitative.

2 Importation et manipulation d’une base de données

4 Analyses bivariées